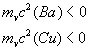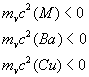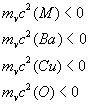 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
9.3. Исследование поля критических температур перехода в сверхпроводящее состояние известных соединений.
Температурное поле перехода керамики в сверхпроводящее состояние, а также в проводящее состояние представлено на графиках рис 88-100 и прилагаемых к ним расчетным таблицам.
Основные выводы из расчета и графического построения следующие. Сверхпроводящие керамики существуют в интервале
изменения стехиометрического коэффициента по кислороду. Рассмотрены керамики 
, где М -символ редкоземельного элемента.
|
M |
Z - заряд ядра |
А - количество нуклонов |
|
|
Y - иттрий |
38 |
89 |
6.2171 |
|
La - лантан |
57 |
139 |
5.577 |
|
Nd - неодим |
60 |
142 |
5.49 |
|
Sm - самарий |
62 |
154 |
5.65 |
|
Eu - европий |
63 |
153 |
5.664 |
|
Gd - гадолиний |
64 |
154 |
6.16 |
|
Er - эрбий |
68 |
170 |
6.1 |
|
Lu - лютеций |
71 |
175 |
5.4229 |
|
Pr - празеодим |
59 |
141 |
5.42 |
- энергия первого ионизационного потенциала эвДля М взят изотоп А с наибольшим процентным содержанием среди других себе подобных изотопов.
Графики качественно повторяют друг друга. Состоят как правило из ветвей, которые имеют максимальную температуру проводимости
и минимальную 0К. Ветви заключены в определенном интервале по изменению Х для каждого состава сверхпроводника.
Характер изменения температуры и протяженность интервала зависят от параметров М. Переход от одной ветви к другой происходит скачком. Изменение Х в пределах 0,001 для параметра Х в районе скачка увеличивает точность максимальной температуры
и величину Х, для которой 
. Скачок по температуре не уходит в бесконечность, а фиксируется конечной величиной 
. Кривые от максимальной температуре сходят до нулевой температуры, проходя величину критической температуры 
. Максимальная критическая температура 
и 0 К определяют фазы сверхпроводящего соединения по кислороду 
.
Фаза металлической проводимости фиксируется интервалом от Х, при котором имеем
мах до Х, при котором имеем мах. Для различных сверхпроводников протяженность фаз меняется, а также меняется их сдвиг по оси Х относительно друг друга.
Значения критических температур определяется НЕОБХОДИМЫМИ условиями. ДОСТАТОЧНЫЕ условия по скорости электронов в зоне проводимости и сверхпроводимости позволяют отделить эти фазы друг от друга.
Для всех соединений проводящая фаза фиксируется НЕОБХОДИМЫМ условием
|
|
cp1 |
Для сверхпроводящей фазы выполняются условия
|
|
cp2 |
Температура Т определяется по формуле (13), в которой обменный квант берется для элемента бария Ba, из предыдущего цикла перед выполнением условий ср2, ср1. Для всех соединений этих сверхпроводников первым отдает электрон в зону проводимости атом бария
Ba.Плавный выход кривой к нулевой температуре сопровождается выполнением третьего и даже возможно четвертого необходимого условия
|
|
ср3 |
Возможен вариант когда все элементы соединения отдают по электрону в зону проводимости и выполняется необходимое условие ср4.
|
|
cp4 |
После выполнения условий ср3, ср4 и происходит скачок температуры и переход на другую ветвь по интервалу изменения стехиометрии кислорода
. Чем выше скачок по температуре тем выше температура перехода в сверхпроводящее состояние. Максимальные значения сосредоточены в узком диапазоне изменения 
/
На крайних ветвях НЕОБХОДИМЫЕ и ДОСТАТОЧНЫЕ условия ср1, ср2,…. Комбинируются так, что их выполнение на протяженности всей ветви не даст критической температуры
. Предельные значения Х на этой ветви фиксируются выполнением условий в нулевом цикле приближения, либо постоянным значением минимального обменного кванта
Мэв.
При переходе от проводящего состояние к сверхпроводящему обязательно соблюдение перехода в НЕОБХОДИМЫХ условиях от СР1 к СР2, СР3… для сверхпроводников, представленных в таблице ДОСТАТОЧНОЕ условие при этом переходе фиксирует резкое увеличение скорости электронов в зоне проводимости по порядку от
до 
см/сек. (Смотри таблицы к каждому графику.) Максимальная скорость достигается при 0 К. При невыполнении условия СР2 при 0К соединение не является при данной фиксированной стехиометрии по кислороду сверхпроводником. При выполнении условия СР3 скорости максимальны и достигают до 
см/сек. В таблицах даны точки перехода при смене НЕОБХОДИМЫХ условий. На графиках точки перехода от проводящего состояния к сверхпроводящему зафиксированы значениями стехиометрического коэффициента по кислороду. В точках смены необходимых условий происходит изменение скорости электронов в зоне проводимости ( смотри таблицы к графикам).
Исследовано температурное поле 5-ти компонентных керамик.
Произведен расчет двух соединений 
Результаты представлены таблично и графически. Интервал изменения Х ориентирован на экспериментальные данные. Для этих соединений выполняются одновременно НЕОБХОДИМЫЕ условия в форме СР1, СP2, СР3, СР4 для первого соединения и для второго в форме СР1, СР3,СР4.
В первом цикле приближения использовались формулы (22а) и (22б), во втором (22) и (22б).Скорость электронов при переходе от условия СР1 (условие проводимости) к условиям СР2, СР3, СР4 возрастала почти на порядок ( см таблицу) . Если для первого условия колебания скорости электронов были в пределах
см/сек, то для условий СР2,СР3,..
см/сек.
Теория не отрицает создание в образцах сложных структур с чередование состояний проводимости и сверхпроводимости. Иногда эти фазы называют фазами Шубникова.
Еще раз подчеркнем особенности температурного поля сверхпроводников выявленные в результате расчета. Зависимость температуры Т от стехиометрического коэффициента по кислороду имеют следующие закономерности.
Зависимость распадается на несколько ветвей. Переход от одной ветви на другую при увеличении Х происходит в критических точках скачком от температуры
до
мах. Интервал перехода по 
и стремится к нулю (в пределах точности расчета по погрешности величины ионизационного потенциала атомов). Переход фиксируется НЕОБХОДИМЫМИ условиями сменой с СР1 на СР2 ( фактический в одной точке Х).При этом происходит уменьшение скорости электронов в зоне проводимости. Падает концентрация носителей тока согласно условию СР1 и падает скорость. Смена скорости это достаточные условия для определения свойств проводника.
Переход от мах до мин 0 К происходит на пологой ветви кривой. При этом ветвь имеет две зоны. Зона металлической проводимости 
и сверхпроводящую зону 
.
Критические точки перехода с одной зоны в другую зафиксированы сменой НЕОБХОДИМЫХ условий с СР1 на СР2. Увеличивается концентрация носителей электрического тока и возрастает скорость. Изменения происходят в узком интервале по Х (
). Достаточные условия фиксируются изменением скорости электронов в зоне проводимости.
Для соединения
проверены две точки с максимальной точностью расчета.
см/сек
Первая точка отличается от второй на 
Скорость возрастает в 3,12 раз. Это переход от металлической проводимости к сверхпроводимости. Разность температур составляет
. В переводе на энергию это составляет 0,0000534эв.
Вторая точка.
см/сек
, Скорость возрастает в 2,19 раз. На переход затрачивается 1,1эв.
Известно, что электроны в атомах обладают энергиями в десятки ЭВ. Сверхпроводимость разрушается при 
эв. Эта энергия и соответствует расчету изменения энергии при смене НЕОБХОДИМЫХ условий при изменении свойств проводника.
Таким образом, вопреки теории БКШ - теория Бардина - Купера - Шриффера 
о куперовских парах, рассчитана другая версия разрушения сверхпроводящего состояния. Версия согласуется с расчетом температур сверхпроводящего перехода. В теории БКШ этого не удалось сделать.
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com