1.2.2.G. Тригонометрические и гиперболические функции в пространстве Y

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

В плоскости комплексного переменного z тригонометрические функции определяются через функции sin(z), cos(z), которые выражены формулами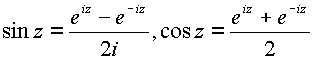

, которые являются следствием формулы Эйлера. Мнимая единица j отличается от мнимой единицы i только обозначением. В пространстве Y эта единица фиксирует третье координатное направление. Алгебра этой единицы совпадает с алгеброй мнимой единицы i. Поэтому в силе остаются и формулы

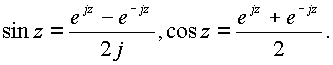Далее формулы распространяются в пространство .

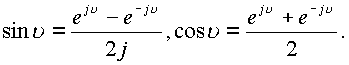При переходе от к получаем гиперболические функции в пространстве Y.

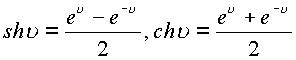
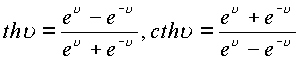
Гиперболические функции выражаются через тригонометрические

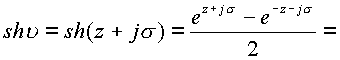
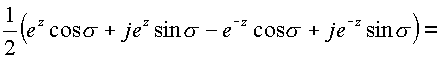
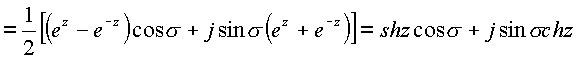Особенность этих формул заключается в том, что они представляют функции от двух комплексных переменных z,,в силу комплексности переменной .Это позволяет получить ряд зависимостей. Например

. Аналогичные преобразования дают

. Определим первый модуль

, так как известно соотношение в комплексной плоскости

Комплексный аргумент будет равен

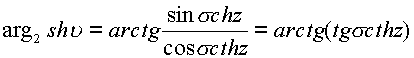
Можно продолжить выделение модуля от четырех переменных

, однако ввиду громоздкости и элементарности выкладок в настоящий момент это не представляет интереса.

Исследуем поведение функций sinn и cosn в особых точках пространства на множестве элементов делителей нуля. Рассмотрим функцию sin(i± j) как функцию от суммы двух углов i и j

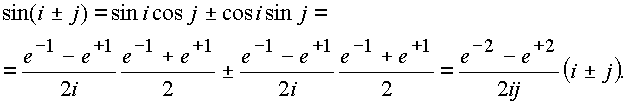
Расшифруем полученный результат. Функция принадлежит элементам делителей нуля:

Квадрат sin(i± j), равный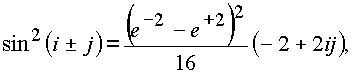

также принадлежит элементам делителей нуля.

Определим аналогично функцию cos(i± j):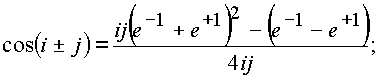

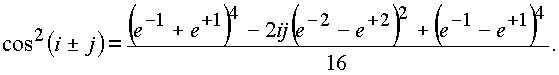
Таким образом, функция cosn , определенная на элементах делителей нуля, не принадлежит этим элементам. Модуль комплекса cos(i± j) не равен нулю и неравен 1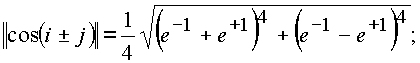

Таким образом, функции sinn и cosn - основные тригонометрические функции, приобрели в пространстве новые свойства, сохранив прежние, присущие им в z-плоскости и на действительной оси без изменения.

Основное тригонометрическое равенство осталось без изменения и на выколотой оси

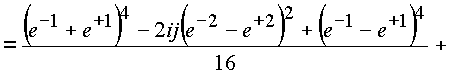
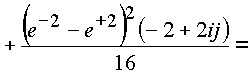
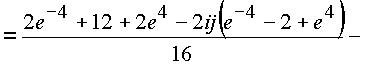
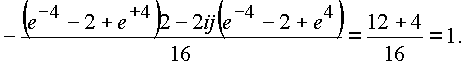
Итак,

Новые свойства функций sinn и cosn определяют и новые свойства остальных тригонометрических функций. Например,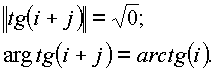

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com