 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
Продолжение 2 из 3.
7.8. Расчет модели атома водорода.
В этом случае орбита состоит из двух сферических оболочек, одна из которых повернута относительно друг друга на угол
Но комплекс 
также содержит изолированное направление и поэтому необходимо рассматривать вариант
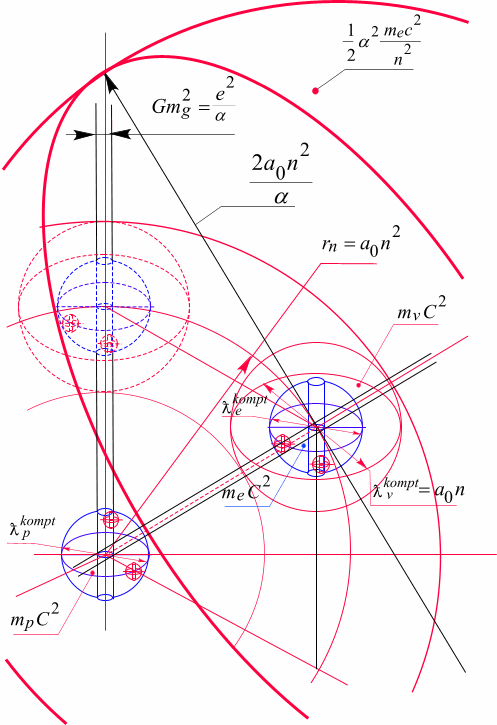
Рис. 68. Модель атома водорода.
, который показывает, что орбита электрона состоит из двух сфер, поверхности которых образуют между собой пространство заполненное пространственными сферами предыдущего измерения ( можно выразиться для наглядности спинорами, напоминающими вращающийся электрон). Это сферическое пространство имеет толщину 
.
Геометрически наглядное представление об оболочках дают рис 9,10,11 главы 1.
Итак, в комплексном пространстве, в котором соблюдается интервал Миньковского, орбита электрона представляет сферическую оболочку, принадлежащую пространству делителей нуля или гравитационно- электромагнитному лучу рис 68.
Протон, находясь в центре, создает искривление пространства. Это искривление как было обосновано является следствием особенности в начале координат, которую можно оценивать комптоновской длинной волны протона
. Масса и энергия протона определяется этим искривлением пространства 
.
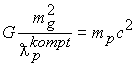Полевая энергия протона создает искривление пространства, которое в бесконечности исчезает ( комплексные координаты переходят в декартовые без особенности в начале ).
Орбиты электрона находятся на расстояниях, в которых искривление пространства соответствует энергии взаимодействия протона с электроном.
Комплексное пространство взаимодействия в соответствии с комплексной алгеброй и
Геометрией обладает структурой. Структура отвечает интервалу теории относительности. Пример формирования структуры приведен в главе 4 (рис 48) Компактизация пространства с ростом его много связности). Этот пример показывает, что не одна частица не может быть рассмотрена как точечная. Нельзя не один элемент структуры стянуть в точку, чтобы она не содержала объем. Поэтому нельзя ни электрон ни протон нельзя принимать как точечные объекты.
В соответствии с правилом квантования орбит Бора в стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь квантовые значения момента импульса, удовлетворяющие условию
, где г-радиус орбиты.
При 
, имеем первую боровскую орбиту 
. Элементарные преобразования по известным формулам дают 
.
Откуда имеем
.
Рассмотрим квантование момента импульса с позиции предельного соотношения гравитационного луча. Заменим значение массы электрона через его значение
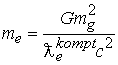получим 
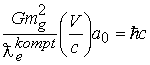, далее применим формулу 
получим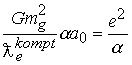 
. Проведем сокращение на предельное равенство
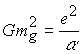получим 
.
Таким образом, на первой боровской орбите выполняется предельное соотношение гравитационного-элетромагнитного луча. Это говорит о том, что первая боровская орбита принадлежит пространству делителей нуля, которое эквивалентно полевому пространству взаимодействий.
Далее рассмотрим орбиты при
. Первый вариант
Преобразуем также динамическое соотношение
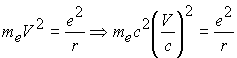
Воспользуемся предыдущим выводом, получим
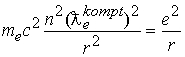откуда имеем радиус орбиты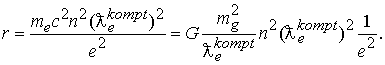 
Сокращая последнее равенство на предельное соотношение получим
Таким образом, видно, что радиусы орбит растут пропорционально квадрату целых чисел.
В атомной физике радиусы орбит определяются по формуле
при Z=1. Покажем, что это выражение отвечает предельному соотношению гравитационного луча. Проведем последовательно преобразования
.
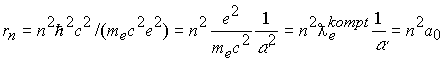Следовательно стационарные орбиты принадлежат пространству делителей нуля( изолированному направлению, световому конусу, гравитационно-элетромагнитному лучу…).
Стационарные орбиты (рассматривая их как траектории электрона) в цилиндрических координатах представляют траектории описываемые мнимым радиусом. В сферических координатах радиус становится равным
. Полевая энергия, удерживающая электрон на стационарной орбите, также разлагается в этих точках на две составляющие, равные по величине и повернутые относительно друг друга на 90 град.. В результате электрон на стационарной орбите не имеет суммарной энергии.
Предельное уравнение гравитационно –электромагнитного луча было выведено при условии равенства гравитационной силы (закон Ньютона) силе электрического взаимодействия двух зарядов (закон Кулона). При этом взаимодействие рассматривалось для точечных частиц. При рассмотрении взаимодействия неточечных частиц была получена формула связи массы частицы через массу фундаментальной постоянной и комптоновскую длину волны этой частицы. Расчеты совпали с эксперементальными данными. Исходя из этой формулы кинетическая потенциальная и другая форма энергии может быть выражена через эти величины. Если имеем
, то можно записать 
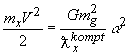, откуда имеем
.
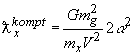Полная энергия точечного электрона на орбите может быть выражена в виде
, условие динамического равновесия для точечного электрона на круговой орбите радиуса 
имеет вид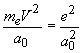 
. Из этих уравнений следует 
.
Кинетическая энергия составляет половину потенциальной энергии.
В комплексных пространственных координатах электрон рассматривается не как точечный объект. Уравнение для полной энергии запишем в виде
.
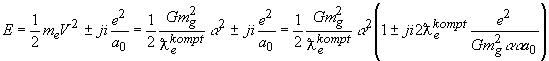Далее имея условия в виде
, а также, что кинетическая энергия составляет половину потенциальной энергии будем иметь
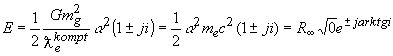
Из этой формулы следует, что взаимодействие электрона с протоном происходит по изолированному направлению радиуса
. Энергия системы состоит из двух равных составляющих, повернутых относительно друг друга на 90 град.. Энергия не имеет суммарной составляющей на орбите. Электрон не может излучать энергию при движении по стационарной орбите, так как его энергия по модулю на точках орбиты равна нулю.
Для перехода с орбиты на орбиту необходима энергия той же структуры, т.е фотон.
Только в этом случае составляющие энергии одновременно изменятся на одну и туже величину.
, где 
- частота фотона.
Далее, используя оператор взаимодействия, оценим энергию обменного кванта или ту полевую энергию, которая создавая искривление пространства, заполняет его гравитационной волной, которая и удерживает электрон на орбите ( или систему электрон- протон ).
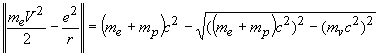
Учитывая большую разницу в массах протона и электрона, а также что сумма энергии протона и электрона превышает величину обменной полевой массы
, последовательно оценим выражение 
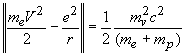. На первой боровской орбите кинетическая энергия электрона меньше потенциальной в два раза и по модулю равна постоянной Ридберга, поэтому величина полевой энергии равна
или в граммах имеем 
Энергия обменного кванта есть полевая энергия и поэтому она в комплексном пространстве представима в виде
. Энергия обменного кванта реализуется через изолированное направление. Реализация идет без потерь (без излучения), так как ее модуль равен нулю. Используя формулу связи комптоновской волны с фундаментальной массой и массой частиц, получим комптоновскую длину волны полевой энергии 
.
Фотон как носитель полевой энергии взаимодействует в изолированном
-туннели с полевой обменной массой, изменяя ее энергию 
(ясно, что могут быть и другие комбинации со знаками плюс и минус, но на этом пока не задерживаем внимание)
Изменение энергии электрона при переходе с орбиты на орбиту можно рассчитать через оператор взаимодействия выведенный на основе пространственной комплексной алгебры, которая учитывает принципы теории относительности. Кинетическая и потенциальная энергия электрона на орбите есть проявление энергии дефекта массы при взаимодействии электрона с протоном. Оператор как было показано выше позволяет рассчитать полевую энергию взаимодействия электрона с протоном, идущую через изолированное направление системы.
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com