1.7.1. Элемент площади в комплексном пространстве

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

В комплексной плоскости (Z),если функция g(z) дифференцируема в односвязной области D и ее производная непрерывна в D, то интеграл от g(z) по любой замкнутой кривой g , лежащей в области D и охватывающей эту область равен нулю: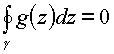

Это утверждение является следствием выполнения условий Коши-Римана

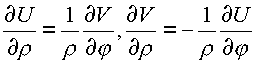где

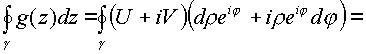
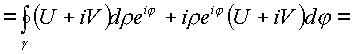
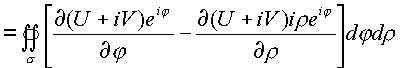
В интеграле по замкнутому контуру в соответствии с утверждениями параграфа сделаем переход к двойному интегралу, считая мнимую единицу i обычным постоянным числом, так что последовательно будем иметь

Где есть область в плоскости комплексного переменного в границах замкнутого контура .

Продолжая преобразования, под знаком двойного интеграла получим следующее выражение.

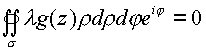
где

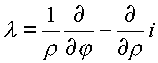
Если функция является аналитической в области исследования, то оператор от этой функции равен нулю, так как, действуя этим оператором на функцию, получаем разность равных производных в двух направлениях.

Элемент площади определяет элементарную площадку с вращением по углу j . Если угол j изменяется в пределах 0< < 2,то элементарная площадка будет представлять кольцо шириной .Определим выражение элементарной площадки в плоскости (z) как проекции элементарной пространственной площадки ds .

В пространстве (n ) элементарная площадка представлена была ранее как произведение

где и, следовательно, имеем

последовательно проведем преобразования по законам пространственной алгебры с целью определить первую действительную часть как проекцию на плоскость (z)

Так как в пространстве .

Первая комплексная часть полученного выражения равна

Аргумент j в сферических координатах согласно формуле параграфа имеет коэффициент равный ?. Поэтому с точностью до постоянного числа i имеем

постоянная мнимая единица i учитывается как коэффициент перед двойным интегралом в произведении j i.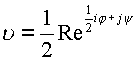

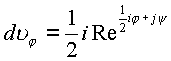
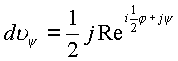поэтому 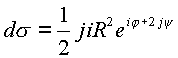откуда следует

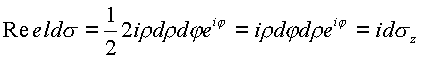
Двойной интеграл в пространстве (, определенный по формуле

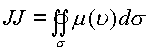переходит в двойной интеграл от функции ,при стремлении второго

пространственного аргумента к нулю

[Следующий параграф]

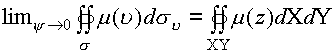
Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com