 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
4.3. Модель вихревого энергетического взаимодействия в пространстве. Физическая трактовка интегралов Коши.
Формулы Коши, реализованные в пространстве
(1.52, 1.56) устанавливают связь между границей области, заданной в виде замкнутой простой пространственной кривой С, либо в виде поверхности, натянутой на эту пространственную кривую без точек самопересечения, и значением функции в любой точке области, охватываемой этой границей.Методы комплексного пространства распространимы в
любое число измерений. Естественно, что для любого числа измерений можно установить единственную связанность наподобие той, которая приводит к интегральным равенствам Коши. В частности, интеграл Коши в n-мерном пространстве будет равен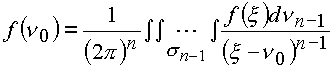
где
Этот интеграл будет определять n-мерный вычет, как
коэффициент C-n и разложении аналитической функции в ряд Лорана в n -мерном пространстве. Эта формула - аналог формулы ( 1.56)В n-мерном пространстве можно указать единственную связность, заданную кривой
С3, на которую без точек самопересечения можно натянуть поверхность так, чтобы она охватывала объемы, которые заключены в аналогичных кривых и натянутых на них поверхностях, меньших по величине размерности пространств. Пространство становится многосвязным. Аппарат позволяет исследовать структуру формирования вложенных друг в друга пространств. Каждая размерность имеет свое количество изолированных e -туннелей, которые могут проникать друг в друга или формироваться в определенной последовательности.Вскрытие причины определенного порядка расположения
e -туннелей есть путь к установлению самосогласованности полей взаимодействия, либо к установлению структуры формирования материи.Основным условием для вывода интегральных теорем
служит условие аналитичности функции в пространстве связной области. Это условие выделяет данную область с кривой С3 и изолированным e -туннелем как особую точку в пространстве большего числа измерений . Внутри этой области существуют свой "геодезические" линии наподобие линиям С3, деформация которых определяется жесткими условиями дифференцируемости функций и интегральными соотношениями. Интегральные соотношения в свою очередь получены на основе тех связей между областью и границей, которые задаются формулами Стокса, Грина, Остроградского. Комплексный n-мерный анализ распространяет эти связи на любое число измерений, открывая тем самым путь к исследованию формирования структуры пространства, заложенной в комплексной пространственной алгебре и ее координатном выражении. Необходимо доказать, что это формирование адекватно отражает реальное формирование материи.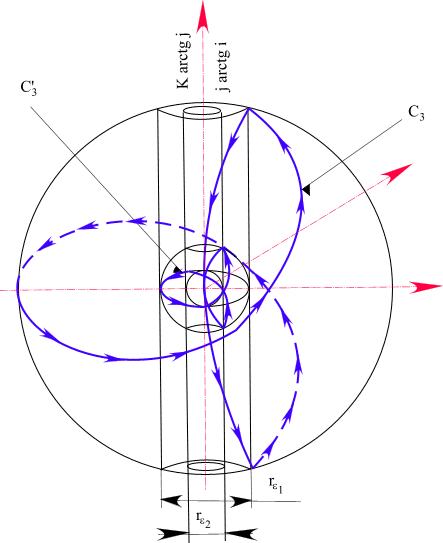
Рис. 47. Взаимодействие двух пространств. Одно пространство можно рассматривать как оболочку ядра другого пространства
На рис. 47 показана модель пространства, которая характеризует пространство как структуру вложенных друг в
друга вихрей, связанных единой "геодезической" кривой С.Изолированные направления этих структурных вихрей
могут как замыкаться в пространстве, так и выходить из него в пространство, большего по размерности, В первом случае пространство будет нейтральным, во втором заряженным, В частности, не отступая от наглядности в изложении, на примере рис. 48, можно пояснить возможные варианты заполнения пространства вихрями. Возможно проследить следующие варианты.Идет заполнение пространства С
3 (условно принят вихрь за кривую С3) вихрями С'3 и только после плотной упаковки, которая может быть определена, энергетическими критериями, идет заполнение пространства С'3 вихрями С"3:При этом также возможны варианты; заполнение одного из
пространств С'3, до полной упаковки и после этого заполнение всех С'3 идет параллельно. Физические условия определяют какой из вариантов реализуется в материи.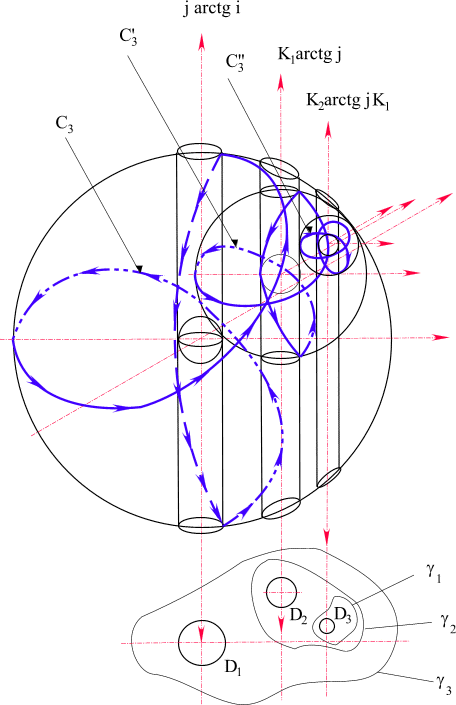
Рис. 48. Компактизация пространства с ростом его многосвязности
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com