 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
Продолжение 3 из 3.
7.8. Расчет модели атома водорода.
Экспериментально установлено, что масса протона, которая значительно превышает массу электрона, может быть введена в формулы только как уточнение результатов. Поэтому энергию электрона на n-1 орбите через оператор следует записать в виде
, где обозначено 
-за полевую энергию изолированного направления.
Для n будем иметь
. Изменение энергии при переходе с орбиты на орбиту равно
Полевая масса естественно меньше массы электрона. При превышении полевой массы массы электрона происходят изменения в самой системе. Поэтому рассматривается случай когда электрон не теряет в атоме своей индивидуальности. Ограничиваясь формулами приближения квадратных корней будем иметь
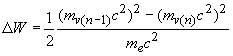
Таким образом, изменение энергии электрона при переходе с орбиты на орбиту происходит вследствии изменения полевой энергии взаимодействия. При переходе происходит изменение частоты
. Соответственно энергия перехода равна 
, где 
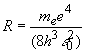- постоянная Ридберга была определена из принципа соответствия результатов квантомеханического и классического решения. Здесь постоянная приведена с характеристикой среды (
-диэлектрическая проницаемость среды). Без ее учета постоянную Ридберга будем применять в классическом выражении 
.
Через оператор взаимодействия определим полевую обменную массу для
n –орбиты. 
.
Можно использовать два варианта расчета. Первый
. Откуда имеем
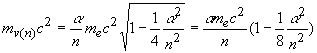Второй вариант, если сразу разложить квадратный корень
Проанализируем результат. На первой боровской орбите отношение скорости электрона к световой скорости равно 
.При переходе на n-орбиту скорость падает в n-раз. Энергия обратно пропорциональна квадрату главного квантового числа n Поэтому при n=1 имеем энергию полевого кванта на первой боровской орбите равной 
. Так, что постоянная тонкой структуры определяет часть энергии электрона, которая служит обменным квантом или полевой энергией, которая удерживает электрон на первой боровской орбите. Используя предельноек выражение гравитационно-электромагнитного луча рассчитаем комптоновскую длину обменного кванта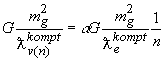 
. Откуда получаем
.
Таким образом, комптоновская длина волны обменного кванта равна радиусу орбиты на которой находится электрон. При
имеем
.
Для уточненной формулы имеем
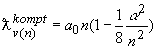. Частота обменного кванта, определяющая переход электрона с орбиты на орбиту будет равна 
. Подставляя полученные данные в равенство, которое было выведено с использованием оператора взаимодействия и проведя преобразования получим
Скорость на орбите 
( это вытекает из динамического уравнения равновесия) Поэтому имеем 
В квантовом условии Нильса Бора скорость на
n-орбите меньше скорости на первой боровской орбите в n раз, орбита радиуса
. Подставляя эти данные в полученное уравнение будем иметь 
или соблюдая соотношения между скоростью и радиусом орбиты получим 
. 
Таким образом, выведено квантовое условие Нильса Бора, которое утверждает, что
В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь квантовые значения момента импульса, удовлетворяющие условию
В пространстве Минковского интервал 
есть величина выражаемая как корень квадратный из разности суммы квадратов пространственных координат
и квадрата временной координаты 
. В комплексном пространстве это выражается в виде
. Временная координата отвечает за сокращение модуля пространства при переходе от одной размерности к другой. В сферических координатах при равенстве 
запись показывает, что в начале координат есть комплексная особенность в виде сферы радиуса 
ввиду наличия изолированного направления 
.Дефект этого сокращения выражается в виде 
. При замене пространственных и временных координат на энергетические массы частиц определяет дефект массы взаимодействия. Для системы водород-электрон имеем 
, где 
энергия ионизации. При образовании систем полевая энергия 
характеризует энергию, идущую на искривление пространства. В системе водород –электрон полевая энергия обменного кванта характеризует искривление пространства орбиты электрона. Искривление определяется комптоновской длиной обменного кванта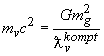 
. Протон бесконечной массы в центре системы вызывает искривление равное 
, которое убывает с ростом радиуса орбиты 
. Кинетическая и потенциальная энергия электрона на орбите соответствуют по энергии искривлению пространства на орбите. Согласно оператора взаимодействия имеем 
. Переходя к комптоновским длинам волн будем иметь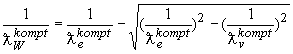 
. Вычислим в первом приближении корень квадратный 
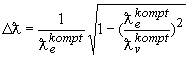. Подставим величину комптоновской длине волны обменного кванта, определенную выше 
получим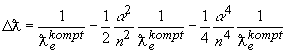 
.
Переходя к энергии связи электрона на орбите получим
.
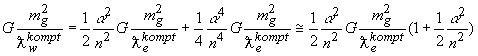Ограничиваясь рассмотрением первого члена разложения получим
,, получим в точном соответствии с расчетами теоретической физики. Второй член дает поправку, совпадающую с поправкой Дирака по степени 
.
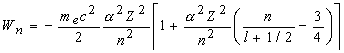
На рис 68 представлена модель атома водорода. Наклонный гравитационно-электромагнитный луч представлен в цилиндрических координатах. Электрон находится на орбите, которая представляет из себя сферическое кольцо, образованное полевой материей обменного кванта с длиной волны 
и создающий вокруг электрона прогиб пространства, который отвечает длине волны энергии связи электрона на орбите 
.Система водород-электрон имеет в центре координат ( где находится водород) комплексную особенность равную длине волны протона .На расстоянии равном орбите электрона комплексная особенность сокращается до длины волны энергии связи электрона с водородом 
.Все эти особенности принадлежат пространству делителей нуля, то есть пространству двух взаимно перпендикулярных векторов, имеющих мнимый радиус в цилиндрических координатах. Каждая точка этой сферической орбиты имеет свой мнимый радиус. Масса обменного кванта находится в другом измерении по отношению к измерению пространства, в котором находится электрон.
На рис 68 это представлено сферой обменного кванта, который заполняет сферическое пространство орбиты. Для стационарных орбит прогиб пространства постоянен. Энергия электрона и обменного кванта в сферических координатах на стационарных орбитах равна по модулю нулю и имеет бесконечное изолированное направление гравитационного луча, на котором она фиксируется радиусами орбит. Итак орбиты электронов представляют пространство между сферическими оболочками, раздвинутыми на расстояние равное комптоновской длине обменного кванта равному 
.
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com