3.2. Энергия в пространстве

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

3.2. Энергия в пространстве

Пространственно-временные координаты, введенные теорией относительности, позволяют записать основные уравнения движения в четырехвекторной форме.

Рассмотрим, к каким последствиям приводит запись этих четырехвекторов в комплексном пространстве. Если взять вектор скорости

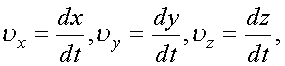
то, чтобы превратить эти векторы в систему четырех пространственно-временных координат, эти векторы делят на величину

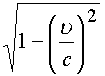
так, что четырехвектор скорости записывается в виде [9]

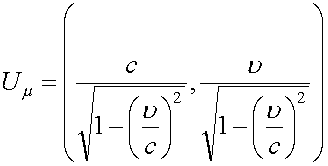Видно, что один из компонентов чстырехвектора всегда больше скорости света. Это одно из противоречий, которое необходимо преодолеть математическому описанию теории относительности. В комплексном пространстве эта матрица запишется в виде

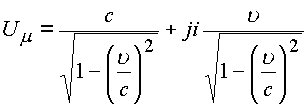
и преобразуется по законам комплексной алгебры

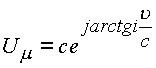(3.3.)

Таким образом, в сферической системе координат скорость 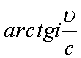системы К выражается как вектор с модулем, равным скорости передачи возмущения в среде, и аргументом, выраженным функцией , где u - скорость в системе К. Это выражение показывает, что с какой бы скоростью u ни двигался объект в системе К, волна от него будет распространяться со скоростью возмущения Даже если 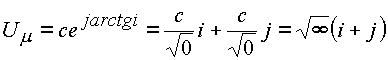, то имеем

Соотношение показывает, что даже при скоростях, равных по осям координат бесконечной величине, волна взаимодействия имеет конечную скорость, равную скорости взаимодействия.

Здесь необходимо признать, что взаимодействие объектов друг с другом рассматривается как взаимодействие пространств различной по величине размерности.

А пространства разного уровня размерности могут взаимодействовать только через -туннели. Каждый имеет свою предельную скорость , возможно не равную с.

Явления на бесконечности переносятся в ограниченный объем сферы радиуса с c выколотым -туннелем. Скорость объекта определяет угол распространения этого возмущения. Если скорость попытается превзойти скорость возмущения, то суммарный вектор повернется на угол p /2 (рис. 41), стремясь удержать объект на данном уровне пространства по измерению.

Если скорость , то вектор скорости направлен по изолированному направлению

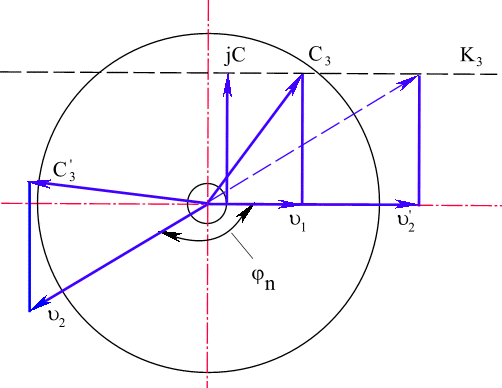
Рис. 41. Многомерность физического пространства, вызванная ограничением величины скорости взаимодействия до предельной скорости света

С вектором скорости тесно связаны уравнения для энергии импульса.

В теории относительности имеем:

;

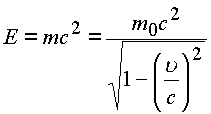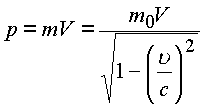где - масса системы К', движущейся относительно системы К со скоростью u ; m - масса в системе К.

В комплексное пространстве (Y) четырехвектор энергии импульса запишется в виде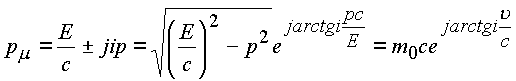

Выражение показывает, что с какой бы скоростью u ни двигался объект-система K' в системе К ее модуль, модуль импульса, постоянен и равен величине .

Из условия равенства комплексных чисел получаем известные соотношения теоретической физики между массой , энергией Е и импульсом p частиц:

;

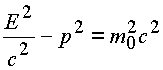из равенства модулей

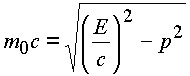
из равенства аргументов

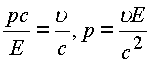Импульс в комплексных координатах описывает сферу радиусом 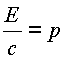. Если энергия равна импульсу , когда , то

(3.4.)

Соотношение (3.4) вводит размер -туннеля в комплексном пространств для частиц квантовой механики.

Диаметр -туннеля равен характеристической величине частицы в координатах импульса

(3.5.)

Энергия частицы, движущейся со скоростью света, разлагается на два взаимно перпендикулярных несуммируемых вектора, имеющих свое начало в двух разных точках окрестности -туннеля. Туннель диаметра заключает в себе изолированное направление , характеризует частицу исходной массы покоя . Все это говорит о том, что пространственно-временные координаты вскрывают наличие в природе мирового осциллятора, непрерывно посылающего в пространство волны энергии, как только скорость отдельных частей материи переходит через скорость света . Выбросить механизм такого перехода от до означает выбросить механизм движения материи.

Выразим энергию через комплексный импульс и комплексную скорость .

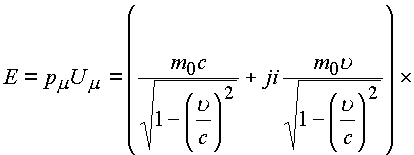
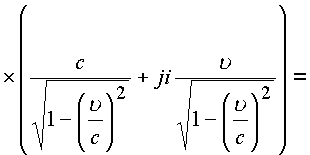
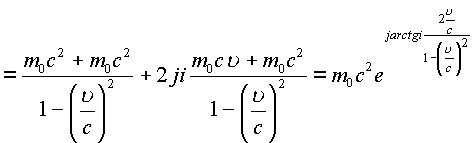Таким образом

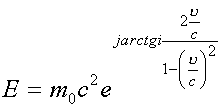
Энергия согласно этим преобразованиям представляет геометрически в пространстве сферу, ядро которой есть пересечение двух изолированных e -туннелей радиуса и которое в свою очередь окружено мнимой сферой комплексного радиуса.

Эйнштейновская формула энергии

есть модуль энергетической сферы .

Энергия частицы определяется двумя энергетическими векторами:

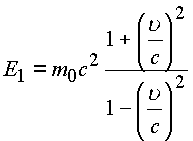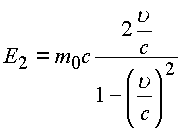Если 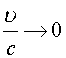, то имеем формулу Эйнштейна

Если 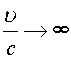, то опять возвращаемся к формуле

Если 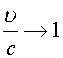, то получаем выражение

Таким образом, при превышении скорости света вектор энергии поворачивается в пространстве на угол p по энергии E₁ и на угол p /2 по энергии Е₂. Формула Эйнштейна есть частный критический случай в природе.

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com