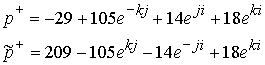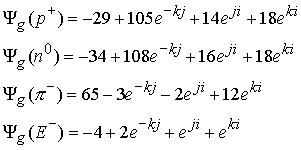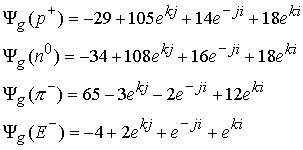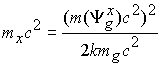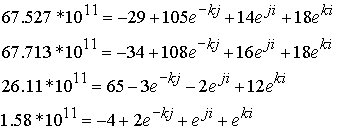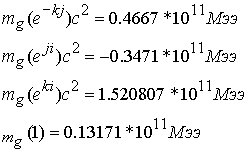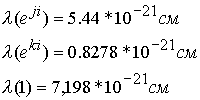Продолжение 2 из 3. 8.8. Сумма единичных глюонных вихрей с весовыми коэффициентами определяет структуру поля микрочастицы

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

Продолжение 2 из 3. 8.8 Сумма единичных глюонных вихрей с весовыми коэффициентами определяет структуру поля микрочастицы.

Комплексное пространство определило симметрию, которая отвечает за это фундаментальное свойство заряда быть положительным и отрицательным. Знак заряда не зависит от положения заряда в пространстве, находится заряд в верхнем полупространстве или в нижнем полупространстве. В связи с этим понятие изоспина можно уточнить. Изоспин введен в формальном вспомогательном пространстве с условными осями , которое называется изотопическим. Комплексное пространство не является формальным пространством и не имеет трех линейных осей. Комплексное пространство обладает и свойством формального изотопического пространства. Понятие изотопического спина увязано с зарядом, который определяется зарядом глюонного поля и знаками весовых коэффициентов, с которыми глюонные поля входят в суммарное глюонное поле микрочастицы. Исследование изоспина пионного триплета уточняет знак изоспина: для обозначения изоспина используем принятые обозначения в квантовой механики микрочастиц .

Изоспин положителен для частиц, у которых глюонное поля электрического заряда определено в верхнем полупространстве (или изолированное направление глюонного поля электрического заряда совпадает с положительным направлением комплексной оси ). Изоспин отрицателен, если его изолированное направление образовано в нижнем полупространстве и совпадает с отрицательным направлением комплексной оси .

Знак изоспина не обязательно совпадает со знаком заряда. Изолированное направление глюонного поля может быть положительным но образоваго в нижнем полупространстве и поэтому изоспин будет отрицательным. И также возможен вариант, когда отрицательный заряд образован в верхней полусфере пространства и его изоспин положителен. Эта симметрия вытекает из моделей главы 8.

Рассмотрим другой вариант стабильной частицы. Протон имеет кварковую композицию . В весовых коэффициентах и единичных глюонных полей эта композиция дает два варианта:

8.8.7

Из этих двух вариантов один дает протон другой антипротон. Это предстоит выбрать.

Антипротон можно образовать кварковой композицией . В весовых коэффициентах гдюонных вихрей будем иметь выражения.

В связи с этим принимаем первое выражение из 8.8.7 за протон, а второе из 8.8.7 за антипротон.

Считается, что протон имеет спин равный +1. Следовательно глюонный электрический вихрь протона даже если он отрицателен, но направлен (или имеет проекцию положительную с коплексной третьей осью в пространстве) и сформирован в верхнем полупространстве то есть имеет положительную величину своего весового коэффициента, то частица имеет изоспин +1 и соответственно положительный заряд.

Протон, определенный через кварковую композицию по определению квантовые числа протона спин, четность, изоспин

Антипротон, определенный через кварковую композицию переходит через операцию зарядовой симметрии (которая неоднократно демонстрируется) в протон

, изоспин которого равен 1/2

Таким образом, протон обладает способностью менять знак изоспина, сохраняя свою массу.

Нейтрон обладает аналогичной симметрией

квантовые числа

Установлено, что в ядерных взаимодействиях протон и нейтрон обладают противоположными изоспинами.

Нейтрон имеет кварковую композицию . Запишем композицию в весовых коэффициентах . По комбинации знаков весовых коэффициентов и вихревых зарядов нейтрон не отличается от протона. Однако он нейтрален и поэтому необходимо рассмотреть разницу в величинах коэффициентах

Вычитая из этой разницы электронное антинейтрино в соответствии со схемой распада нейтрона получим

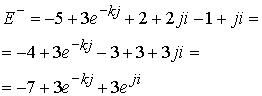
Эта разница определяет весовые коэффициенты распада нейтрального нейтрона на электрон и электронное антинейтрино по схеме, установленной в экспериментах

Согласно этой схеме один из кварков d в композиции нейтрона переходит в кварк u выделяя электрон и электронное антинейтрино, так что электрон равен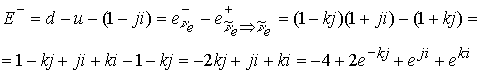

Итак электрон выражается в виде

В первом варианте нет учета кинетической энергии распада, которая составляет разницу в глюонных полях электрона вычисленных этими двумя способами

После определения энергии глюонных полей эта величина была вычислена.

Экспериментальная величина равна 0,762 Мэв. Расхождение составляет 23%.

Таким образом, рассмотрены четыре стабильных микрочастицы

Определены выражения суммарного глюонного поля каждой из частиц через весовые коэффициенты и вихревые единичные зарядовые поля.

8.8.8

Для каждой частицы значения весовых коэффициентов не меняется, если изменить знаки электрического и лептонного вихря.

8.8.9

Установленная симметрия есть следствие равенства масс единичных глюонных полей разных знаков.

8.8.10

Система глюонных полей составлена из наиболее стабильных частиц, для которых исследовано соответствие квантовых чисел физики микрочастиц со структурой этих глюонных полей. Система составлена для четырех частиц и содержит четыре неизвестных в виде единичных глюонных полей и четыре величины суммарного глюонного поля каждой микрочастицы.

Для определения масс зарядовых единичных глюонных полей в системе 8.8.9 необходимо вычислить суммарное глюонное поле микрочастиц. Энергетически микрочастица рассматривается как дефект массы в результате взаимодействия фундаментальных масс . Дефект масс есть в свою очередь следствие образования глюонного поля между взаимодействующими массами.

8.8.11

где к- количество взаимодействующих фундаментальных масс,

-суммарная масса глюонного поля микрочастицы,

- масса частицы.

Формула представляет операционную замену интервала теории относительности на энергетические массы. (глава 7). Формула использовалась при вычислении энергии связи атомных ядер (глава 5), а также при исследовании радиоактивных распадов ядер (глава 6). Сходимость результатов с экспериментальными данными дает основание в применении этой формулы и в дальнейших расчетах.

Если известно суммарное поле микрочастицы, то масса частицы определяется из 8.8.11, если известна массы частицы, то глюонное поле определяется по формуле

8.8.12

Для определения единичных глюонных зарядовых полей, которые через весовые коэффициенты составляют суммарное глюонное поле, используем систему 8.8.9, в которой суммарные глюонные поля определены для стабильных частиц с известными массами.

Если известны единичные глюонные зарядовые массы, то по известным весовым коэффициентам будет определено суммарное глюонное поле микрочастицы и ее масса по формуле

8.8.13

Таким образом, если определить вклад каждого зарядового вихря в глюонное поле микрочастицы с соответствующими весовыми коэффициентами, вычисленными из кварковых композиций классификации микрочастиц и модами распада, то по формуле 8.8.13 вычисляются массы микрочастиц.

Согласно формулы 8.8.12 для наиболее стабильных частиц имеем:

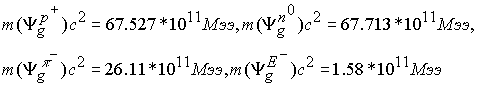
В результате из 8.8.9 имеем систему

8.8.14

Решение системы 8.8.14 дает следующие значения величин единичных зарядовых вихрей.

8.8.15

Рассмотрим энергетическую структуру кварков на примере

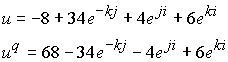
Определим радиусы изолированных 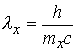-туннелей заряженных глюонных вихрей по формуле квантовой механики . Для каждого вихря входящего в состав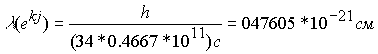 кварка будем иметь:

8.8.16

Теоретическая физика дает величину сечения слабого взаимодействия см. Вычисленная величина радиуса изолированных туннелей зарядовых вихрей находится в полном соответствии с этой величиной. Таким образом, до см Следовательно кварк может рассматриваться как точечная частица до величины этого радиуса. Вещество кварка сосредоточено в объеме радиуса см.

Структура глюонного поля задает квантовые числа и массу микрочастиц.

Исследуем влияние квантовых чисел на структуру и массу микрочастиц на трехкомпонентной кварковой композиции барионов.

Резонанс имеет кварковую структуру , которая задает глюонное поле в виде , которое представляет сумму глюонных составляющих исходного кварка , в котором к лептонной составляющей применена операция сопряжения и отражения. Иными словами тройной поворот лептонного поля дает спин микрочастицы равным , так как исходный спин кварка принят 1/2 в системе расчета. Спин микрочастицы представляет количество поворотов лептонного поля в композиции частицы. Вычисление массы дает величину Мэв. Расхождение составляет 4,1%. Изоспин равен 3/2,

Изоспин определяется электрической составляющей глюонного поля частицы и в этой композиции он равен , так как оно представляет утроенное поле глюонного поля исходного кварка . Кроме того согласно изоспиновой диаграмме рис глюонные (электрическое и лептонное) складываются.

Кварковый состав представлен двумя микрочастицами

Протон входит в систему уравнений, т. е., поэтому имеет квантовые числа .

Поворот глюонного поля в кваркахопределяет суммарное поле композиции

Вычисления дают массу резонанса Мэв. Расхождение составляет 076%. Спин частицы, следуя предыдущим рассуждениям, равен 1/2 изоспин равен 3/2. Однако масса меньше экспериментальной и поэтому необходимо рассмотреть вариант с третьим поворотом глюонного поля в третьем кварке композиции. Тогда будем иметь

. Вычисления дают Мэв. Расхождение составляет 9,3%. Спин равен3/2, изоспин равен 3/2.

Кварковая композиция представлена двумя частицами .

Нейтрон является как и протон исходной частицей для вычислений полей. Поэтому рассматриваем более подробно резонанс.

Если в кварках повернуть (СР) лептонное поле, то получим суммарное глюонное поле композиции в виде

Вычисление массы дает величину Мэв. Спин равен 1/2, изоспин равен 3/2. Четность положительная. .

Если повернуть лептонное поле и в кварке , то получим

Вычисление массы дает Мэв. Расхождение составляет 13%.

Спин резонанса равен 3/2, так как повернуто лептонных составляющих в композиции из трех кварков. Изоспин равен также 3/2, так как имеем электрическую составляющую глюонного поля равную сумме трех электрических глюонных полей. -квантовые числа микрочастицы находятся в соответствии с экспериментальными.

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com