 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
10.6. Особенности комплексной пространственной системы пространственных координат
Необходимо отметить еще одну принципиальною особенность числа, которая является также одним из его важнейших свойств.
В координатном пространстве поле чисел задает точку единственным образом и однозначно как одну независимую переменную.
Известно, что каждой точке
Z на плоскости прямоугольных декартовых координат соответствует пара точек Z=(X,Y).На комплексной плоскости имеем одну точку
Z.Соответственно функция в декартовой системе координат является функцией двух переменных
F(X,Y), в комплексной плоскости имеем функцию одной переменной F(Z).В пространстве соответственно имеем
F(X,Y,Z), в комплексном пространстве
. Таким образом, поле чисел задает для функции одну переменную. Декартовые и другие системы задают для функции массив переменных. Структура точек в декартовой и другой не числовой системе задается дополнительными условиями (например расстоянием между точками).
В комплексном пространстве структура точки определена свойствами чисел и не требует ввода дополнительных условий.
Если в декартовой системе имеем (
X,Y,Z) то ноль определен как массив из нулей (0,0,0) каждой из действительных значений величин X,Y,Z. Таким образом, точка ноль должна обладать как и любая точка пространства той же структурой, чтобы избежать противоречий. Но в этом случае возникает другое противоречие о выходе координатных осей из одной точки.В комплексном пространстве это противоречие устраняется см 1.1.
Система отсчета (система координат) комплексного пространства представляет точку не как упорядоченное множество (массив действительных или комплексных) чисел (компонент, координат)
, а одним числом 
.
В комплексном пространстве функция
Q является функцией одной переменной (числа). Одновременно с этим функция представляет комплекс от функций 
, которые определены через массив чисел 
.
где
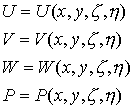
Таким образом, функция
Q, представляет комплексную структуру из функций
, которые являются функциями от массива чисел
и представляют функции от четырех переменных, которые образуют функцию одной переменной.. Структура числа в результате позволяет исследовать структуру пространства, как структуру вложенных друг в друга пространств разных по величине размерностей. Размерность пространства более высокой размерности, описывается числом также более высокой размерности, которое включает в себя числа меньшей размерности, описывающие пространства меньшей по величине размерности. Пространство 
, содержит в себе пространство 
.Открывается возможность исследовать структуру пространства с его количественной оценкой. Такой особенностью не обладают ни векторное ни тензорное пространство.
В тензорной алгебре точка рассматривается как объект, которому по определенному правилу отнесена упорядоченная система
действительных чисел 
(ее координат). Так что точки пространства взаимно однозначно соответствуют точкам некоторой области N-мерного пространства переменных .Число координат, требуемых для определения каждой точки 
, называется размерностью пространства.
Допустимое преобразование координат сводится к установлению
N –новых координат
, связанных с исходными по формуле 
Уравнения должны удовлетворять двум условиям: функции должны быть непрерывно дифференцируемы и
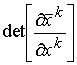отличен от нуля. Функция Q определена фактически массивом координат.
В евклидовом пространстве связь между координатами задается как корень квадратный из суммы квадратов координат.
Изучение электромагнитных явлений привело к открытию псевдоевклидова пространства. Интервал в этом пространстве инвариантен относительно преобразований Лоренца. Пространство и время едины, а геометрия его псевдоевклидова. Бесконечно малый интервал между двумя событиями
является инвариантом в этом четырехмерном мире.
Интервал также записывается в виде
, где в скобках стоит квадрат дифференциала расстояния между двумя бесконечно близкими точками трехмерного пространства. Для декартовых координат имеем 
, для цилиндрических координатах имеем 
(
дифференциал от массива 
, в сферических координатах 
имеем 
.
К настоящему времени сложилось ошибочное устойчивое мнение, что если заданы координаты (
x,y,z) и модуль как корень квадратный из суммы квадратов, то имеем дело с пространством. Это ошибочная точка зрения, так как взаимная перпендикулярность координат введена не внутренним развитием математики ( алгебре чисел), а искусственно. Символы
могут быть определены на одной прямой как переменные, а их модуль есть функция трех переменных.
Если рассмотреть модуль комплексного пространства от трех переменных, то будем последовательно иметь
.
, далее 
Только частный случай приводит к виду интервала применяемому в современных теориях
откуда
В этом случае выражение модуля совпадают с выражением интервала в декартовых координатах. Но в этом случае модуль соответствует структурному трехмерному пространству.
Точка в пространстве задается не массивом
X,Y,Z, а одной структурной точкой.
, где 
, 
,
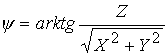где все параметры являются действительными числами.
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com