 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
10.14. Механизм взаимодействия гравитационных полей
Гравитационные массы пробного и тяжелого тела обладают свойством быть заряженными значением одного фундаментального знака заряда. Формула тяготения Ньютона оставляет открытым вопрос о механизме притяжения двух тел одного значения заряда.
Если тело рассматривать в комплексном пространстве, то знак заряда его поля определяется знаком изолированного направления. В простейшем случае можно рассмотреть изолированные направления в комплексных координатах
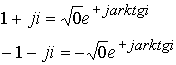
Обменные кванты как мера энергии поля также имеют два варианта направления положительного заряда (в верхнюю и нижнюю полусферу координат) (см. Глава 7, 8, 9).
Гравитационное поле складывается из энергий полей, мерой которых служит обменный квант. В комплексном виде обменные кванты пробного и тяжелого тел равны
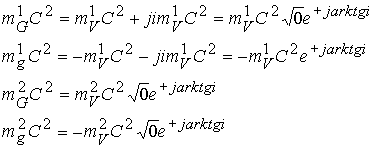
Рассмотрим движение обменного кванта по циклонной кривой
В точке входа в изолированное направление пробного тела величину суммарного обменного кванта рассматриваем во первых как сумму
![]()
Модуль
Аналогично рассмотрим выход из изолированного туннеля пробного тела.
На выходе имеем взаимодействие нижней полусферы пробного тела с верхней и нижней полусферой тяжелого тела, в результате по величинам обменных квантов получим
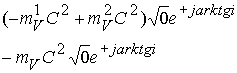
Оценивая по модулю величины обменного кванта на выходе из изолированного туннеля пробного тела, вновь получим движение масс под действием потенциальных сил в сторону тяжелого тела. Таким образом, происходит “зашнуровывание“ (термин взят из ядерной физики) взаимодействующих тел в одной структуре.
Инерциальная масса тела, как было показано в 10.13, определяется комплексом
![]()
где
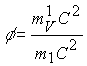
Модуль инерционной массы не зависит от знака обменного кванта (вычитается он из кванта тяжелого тела или складывается с ним), поэтому рассмотренные варианты взаимодействия полей сводятся в расчетах к одному.
Рассчитаем величину дискретного сдвига пробного тела относительно тяжелого.
Взаимодействие происходит непрерывным образом, однако формулы отсекают конкретные дискретные значения. За начальные исходные параметры принимаем
Исходя из этих значений, определяем инерционные массы по формулам
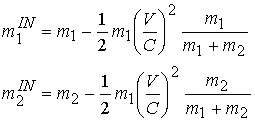
Инерционные массы при переходе в расчете к новым текущим параметрам в формуле потенциала Ньютона становятся гравитационными, поэтому определяем их произведение и сумму, которые входят в рекуррентное соотношение
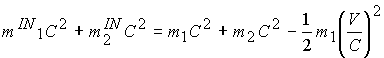
Произведение дает
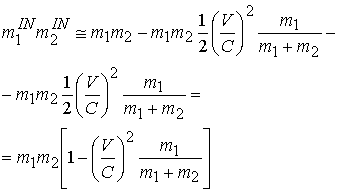
В результате рекуррентное соотношение принимает вид
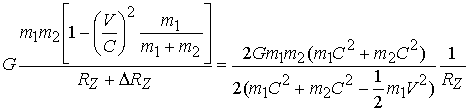
Сокращения дают
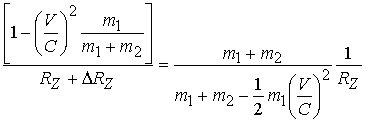
Далее
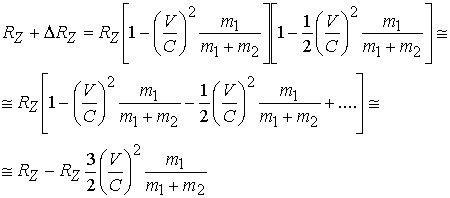
Откуда окончательно будем иметь
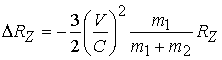
Дальше можно провести расчет уже с новыми значениями параметров и определить
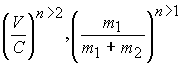 .
.
Преобразуем формулу, введя значение скорости
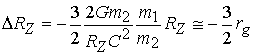
Таким образом, показано, что формула тяготения Ньютона определяет движение пробного тела в поле тяготения тяжелого тела при каждом фиксированном расстоянии на величину равную гравитационному радиусу пробного тела. Это геометрический квант движения. Расстояние изменяется и процесс продолжается.
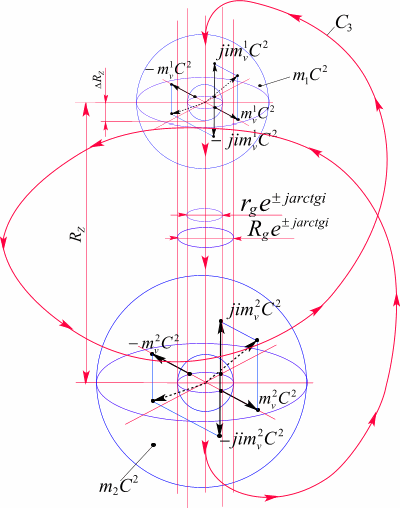
Рис. 101. Смещение пробного тела массой
Поэтому можно ограничиться приведенной зависимостью.
Произведем некоторые промежуточные обобщения.
Современная теоретическая физика применяет математический аппарат, который не адекватен взаимосвязям в реальном физическом пространстве. Эта неадекватность выражается в самом существенном – определении структуры точки в пространстве, не говоря уже о линиях, поверхностях, объемах и так далее.
Современный математический аппарат векторного и тензорного исчисления фиксируют точку в пространстве как набор значений координат. Считается, что значения совмещаются в одну точку, как это происходит в начале координат ![]() . Это допущение не совместимо с изучением явлений микромира и макромира.
. Это допущение не совместимо с изучением явлений микромира и макромира.
Теория комплексного переменного Коши ввела окрестность точки и показала не допустимость такого положения. Например: ![]()
Единица на вещественной оси имеет две границы, а вся вещественная оси рассматривается в комплексном пространстве для этого случая как разрез с двумя границами.
На современном математическом языке структура точки задается набором значений координат. Знаменитые преобразования Лоренца переводят один набор координат
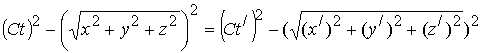
Набор координат с постоянством квадрата интервала является исходным в описании структуры точки в пространстве – времени Минковского. А. А. Логунов использует при выводе преобразований Лоренца приведение квадратичной формы записи интервала в галилеевой системе координат к сумме квадратов. Квадратичная форма записи соответствует скалярному произведению векторов
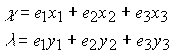
Где
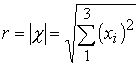 . Однако это лишь гипотеза, которая не соответствует реальному пространству. Уже в пространстве четырех измерений временная координата отличается знаком от пространственной координаты и пространство получило название псевдоевклидово.
. Однако это лишь гипотеза, которая не соответствует реальному пространству. Уже в пространстве четырех измерений временная координата отличается знаком от пространственной координаты и пространство получило название псевдоевклидово.
Таким образом, уже в трехмерном пространстве точка задается набором координат и расстоянием от начала координат точки (0, 0, 0) формулой, которая не является естественным результатом построения трехмерного пространства как перехода от одномерного к плоскости и пространству.
Базисные единичные вектора не подчиняются законам операций над действительными числами. Векторное пространство не является числовым полем. Тензорное исчисление является обобщением векторного и также не является числовым полем.
В ОТО А. Эйнштейна и РТГ А. Логунова квадрат интервала определяется также квадратичной зависимостью с в веденными в него метрическим тензором
При этом в ОТО используется Риманова геометрия, в РТГ рассматривается пространство Минковского. Метрический тензор определяется как зависимость от тензора энергии-импульса при решении гравитационного уравнения. Гравитационное уравнение устанавливает связь между тензором кривизны пространства и тензором энергии – импульса. Это хорошо известные факты. Даже при рассмотрении квадратичной зависимости в виде дифференциалов, структура точки определяется через набор этих дифференциалов, совмещенных в одной точке. Можно конечно стоять на точке зрения, что уравнения и введенный в них тензор энергии импульса (кстати также набор энергий по координатам) откорректирует метрический тензор так, что он будет давать структуру точки в пространстве. Результатом решения уравнения гравитации вновь является выражение для четырехмерного интервала и вновь не соответствует реальной действительности.
Таким образом, в уравнении гравитации нет ни одного параметра, который бы был адекватен реальному физическому пространству.
Задание трех координат не определяет структуру точки. В связи с этим, исследования в микромире ограничены исследованием параметров на входе и выходе, без детализации процесса. Достаточно напомнить вершины диаграмм в теории Фейнмана.
В статье “ Единая теория поля “Вернер Гейзенберг пишет: “ При столкновении двух элементарных частиц очень высокой энергии рождаются многочисленные новые частицы. Было бы плохим описанием этого феномена, если сказать, что частицы разбились на большое число мелких осколков. Гораздо правильнее сказать, что огромная кинетическая энергия частиц преобразовалась при столкновении по закону Эйнштейна в материю, порождая большое число новых элементарных частиц. В самом деле, независимо от индивидуальной природы частиц, участвующих в столкновении, новые частицы всегда принадлежат хорошо известному спектру элементарных частиц. Энергия становится материей, принимая форму элементарной частицы. Спектр элементарных частиц воспроизводит самого себя в процессе столкновения с высокой энергией “.
Таким образом, Вернер Гейзенберг проводит детальное рассмотрение процесса столкновения в точке. Точка в пространстве имеет структуру, которая отвечает образованию любого спектра частиц.
Структура микрочастиц, исследованная по модам распада, опровергает структуру точки как набор координат и подтверждает многоуровневой характер пространства. Так что точка характеризуется вложенными друг в друга пространствами разных измерений.
Теоретическая физика закодировала частицы, наделяя их различными зарядами, массами, названиями, спинами и другими характеристиками. Характеристики не увязаны со свойством пространства (так как нет структуры пространства в точке). До настоящего времени нет определения фундаментального свойства заряда, быть положительным или отрицательным.
В современной теоретической физики сингулярности пространства возникают из за несоответствия физических условий, введенных в решение, с применяемым математическим аппаратом. Это сингулярности типа
Однако Эйнштейн был прав пологая, что частицы – это сингулярности поля в пространстве.
Поле в конечном счете определяет геометрию пространства и структуру материальных тел.
Поэтому математический аппарат исходных пространственных координат должен содержать сингулярность.
В пространстве Минковского сингулярность скрыта в выражении квадрата интервала.
В преобразованиях Лоренца при
Лоренц оставил преобразования как набор координат, поэтому теоретическая физика, не имеющая необходимого математического аппарата, не может записать преобразования в сферических координатах. Конус Света рассматривается фактически в цилиндрических координатах. При выводе своих преобразований Лоренц использовал равенство интервалов, которое в комплексной записи последних может вскрыть гениальность вывода.
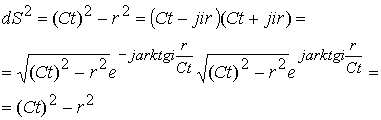
Если
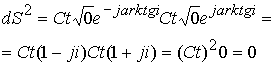
Квадрат интервала раскладывается на два сомножителя, которые характеризуются модулем и аргументом. При выполнении физических условий, когда
Проведенные выкладки и следствия из них показывают, РТГ А. А. Логунова неизбежно опирается на комплексное пространство (но это выражено не явно). ОТО А. Эйнштейна из физической и математической теории превратилась с течением времени в философскую теорию (это лучший вариант для всех теорий, которые дают что-то новое в познании мира).
Таким образом, несоответствие математического аппарата теоретической физике заключено в неверном определении геометрии реального мира. Рост размерности пространства должен являться внутренним естественным развитием математических операций. Переход от вещественных чисел к комплексным в смысле Коши происходит в следствии невыполнимости извлечения квадратного корня из –1. Извлечение корня из +1 в пространстве диктует введение новой единицы, которая не принадлежит вещественным числам, то есть для нее не выполняется операция извлечения корня из –1 и одновременно корень из +1 в комплексной плоскости не дает двух значений. Одновременно находит объяснение и коммутативность умножения элементов, как закон вещественных и комплексных чисел в смысле Коши.
Пространство комплексных чисел является числовым пространством-полем.
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com