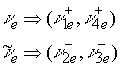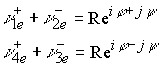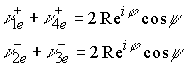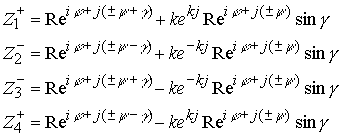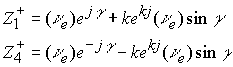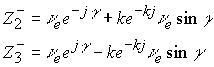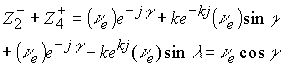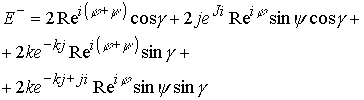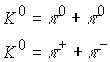Пространство электронного нейтрино является сопряженным пространственным комплексом

Пространство имеет два заряженных подпространства с сингулярными аргументами . Для сокращения записи иногда будем обозначать в виде . Выделим из пространства положительно заряженное подпространство, проведя следующие операции комплексной алгебры

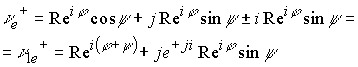
Для сопряженного комплекса будем иметь

Далее также получим

Система из четырех возможных пространств с заряженным подпространством определяет положительный заряд в верхнем и нижнем полупространстве –это

В классификаторе микрочастиц различают электронное нейтрино с положительным лептонным зарядом и отрицательной спиральностью Закодировано как нейтрино

А также электронное нейтрино с отрицательным лептонным зарядом и положительной спиральностью

Закодировано как антинейтрино

Следует принять за

Система (10.16.2) дает возможность оценить взаимодействие пространств разного заряда.

Результат можно трактовать как незаряженное лептонное пространство.

Второй вариант

На рис 102 представлена геометрическая модель нейтрино как единое пространство с положительным зарядом в нижней и верхней полусферах и нейтральным плоским комплексом, повернутым дополнительно на угол в центре осей координат. Этот поворот и определяет знак спиральности: если поворот против часовой стрелки то спиральность отрицательная, по часовой стрелки у антинейтрино спиральность положительная. При движении мнимой точки с сингулярным аргументом по циклонной кривой изменяются углы , что приводит к повороту центрального плоского комплекса. Функции, заданные на кривой удовлетворяют условиям дифференцирования в форме Коши и поэтому циклонная кривая является геодезической кривой.

Кривая представляет плоскую спираль в каждой своей мнимой точке.

На рис 102 представлена геометрическая модель антинейтрино. Обозначения позволяют оценить разницу в свойствах нейтрино и антинейтрино.

В соответствии с формулами (10.16.5), в центре нейтрино или антинейтрино расположен нейтральный комплекс , который отождествляется с нейтральным гамма –квантом (комплексом в смысле Коши). Комплексное пространство и нейтринное пространство дает возможность детализировать процесс аннигиляции: при аннигиляции нейтрино и антинейтрино происходит образование двух гамма –квантов с кинетической энергией, которая реализуется по изолированному направлению

где

Пространство, имеющее один скомпенсированный лептонный туннель по формуле (10.16.5) плюс любая комбинация нейтрино из системы (10.16.2) отождествляется с мюонным нейтрино, например

и так далее. Мюонное нейтрино имеет мюонный лептонный заряд

Скомпенсированный лептонный комплекс представляет энергию аннигиляции, которая удерживается в структуре.

Пространство, имеющее два скомпенсированных лептонных зарядовых подпространств плюс одно электронное нейтрино из системы (10.16.2) отождествляется с Тау-нейтрино, например

Системы (10.16.6), (10.16.7) предполагают увеличение количества скомпенсированных зарядовых подпространств, что приведет к открытию новых названий нейтрино. Зарядовое сопряжение для мюонного и Тау-нейтрино остаются по структуре как у электронного нейтрино.

Модели нейтрино, антинейтрино, мюонного нейтрино даны в координатах

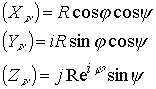
Пространство электрона и позитрона.

Представим пространственный комплекс в виде

и выделим зарядовые подпространства

Структура системы (10.16.10) повторяет структуру системы (10.16.2) на новом более высоком уровне размерности комплексного пространства и одновременно характеризуется новыми свойствами. Положительно заряженный комплекс имеет закрутку комплекса по двум направлениям , так же как заряженное подпространство этого комплекса можно представить в виде

будем иметь

Если пространство , то комплексы отождествляются с позитроном , определенным в верней и нижней полусфере комплексного пространства.

Если сложить комплексы, то в пространстве возникнет скомпенсированный электронный туннель

Электрон отождествляется с комплексами

Незаряженный электронный туннель есть сумма этих комплексов

Рассмотрим также комбинации зарядов

Полученный результат совпадает с предыдущим (10.16.14) при условии, что для положительного заряда в нижней полусфере пространства происходит поворот антинейтрино, так что оно превращается в нейтрино.

Далее

Этот результат является переходом нейтрино в отрицательном электрическом заряде, определенным в нижнем полупространстве (Z) в антинейтрино.

Последовательно выделяя зарядовые пространства электрические и лептонные, получим в общем виде структурное сопряжение зарядовых подпространств электрона в виде

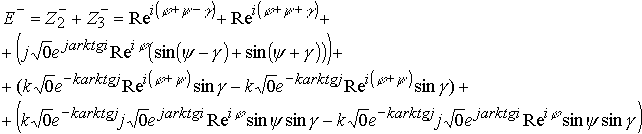
Комплекс представляет сумму комплексов в верхнем и нижнем полупространстве, поэтому его можно записать в виде

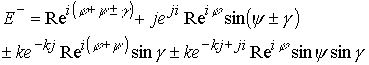
Знак минус относится к нижнему полупространству лептонного и электрического заряда.

Знак плюс минус перед аргументом в комплексах определяет перезарядку нейтринного пространства относительно электрического в зависимости от положения в верхнем или нижнем полупространстве мнимых электрических точек, поэтому если повернуть угол в третьей и четвертой скобки у вторых членов, то сокращение не произойдет и получим комплекс

Ядро электрона представляет комплекс (первый член) в смысле Коши, электрон имеет лептонный положительный заряд (второй член), электрический заряд (третий член комплекса), смешенный лептонно-электрический заряд (четвертый член комплекса). Структура сопряженных зарядовых пространств электрона пояснена на рис 105.

Таким образом, один оборот по аргументу, определяющему заряд электрически заряженного подпространства имеем два оборота нейтринного пространства. Это и обеспечивает возможность переориентации нейтринного пространства при переходе из нижней полусферы в верхнюю в пространстве . Структура заряженных подпространств представлена на рис в координатах

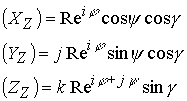
Ядро электрона представляет пространство нейтрино и может быть заряженным и нейтральным. Электрически заряженное подпространство включает лептонное подпространство в вершинах своих мнимых точек.

Аннигиляция электрон –позитронной пары также детализируется

где

В пространстве пространство являясь изолированным пространством одновременно имеет свои степени свободы по структурированию.

Пространство может входить в пространство как нейтральное

Рассмотрим комплекс

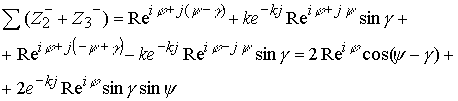
Комплекс можно отождествить с отрицательно заряженным пионом

Положительно заряженный пион не имеет нейтринного заряда и поэтому представляет сумму положительно электрически заряженных пространств с компенсированными нейтронными комплексами

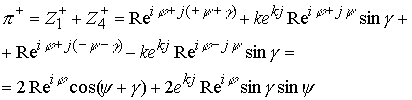
Окончательно

На рис 106 представлено зарядовое сопряжение подпространств отождествляемых с заряженными пионами .Заряженный пион представляет заряженное электрическое подпространство, в котором лептонные заряды скомпенсированы и равны нулю. Пион не имеет лептонного заряда. В центре пиона расположено ядро из пространства нейтрино, электрические мнимые точки представляют также пространства нейтрино – нейтральное. Центральное ядро имеет вращение верхней и нижней полусферы в разных направлениях. Мнимые точки электрически заряженного подпространства также имеют вращение около оси , как показано на рис.

Мюонное нейтрино определено по формуле (10.16.6), Тау-нейтрино по формуле (10.16.7). Пространство мюона будет представлено в виде

Соответственно имеем

Структура Тау-лептона по формуле соответствует замене электронного нейтрино на тау-нейтрино в заряженном пионе.

Пространство МЕЗОНОВ

Пионы закодированы в микромире как нестранные мезоны. Далее открыт спектр мезонов с зарядом странность-S, очарование-c, прелесть –b.

Структура пространства этих заряженных частиц повторяет структуру лептонного уровня. Частицы с зарядом странности S определены в пространстве с одним скомпенсированным пионным сингулярным туннелем, а именно

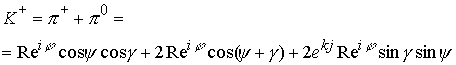
Положительно заряженный - мезон имеет подпространство, которое отождествляется с положительным электрическим зарядом. Других подпространств с зарядами мезон не имеет. Мезон представляет структуру в точном соответствии основному каналу распада.

Нейтральный мезон имеет заряд странность и один скомпенсированный сингулярный туннель, который и определяет наименование этого заряда –S.

В соответствии с каналами распада имеем

Применяя формулы (10.16.17), (10.16.18), (10.16.19), получим разные выражения, однако они не нарушают структурной картины. Второй канал распада идет с большей величиной кинетической энергии заряженных пионов.

Очарованные нестранные мезоны имеют два скомпенсированных сингулярных туннеля, что и послужило кодировки заряда – очарование – с.

[Следующий параграф]