 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
1.7.4. Лемма К. Жордана в комплексном пространстве
![]()
Пусть имеем
1) функция
2) ![]() при
при ![]() где
где ![]() - верхняя полусфера
- верхняя полусфера ![]() Тогда
Тогда ![]()
Доказательство. Заменим в интеграле функцию синус ее представлением в пространстве
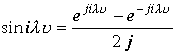 .
.
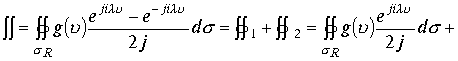
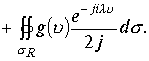 Так, что необходимо исследовать два интеграла
Так, что необходимо исследовать два интеграла ![]() Рассмотрим первый интеграл.
Рассмотрим первый интеграл. 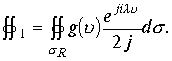 Определим модуль функции
Определим модуль функции ![]()
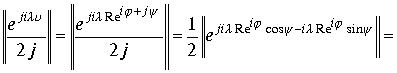
![]()
Пусть
Модуль функции
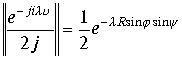 меньше единицы для той части верхней полусферы, для которой аргументы изменяются в интервалах
меньше единицы для той части верхней полусферы, для которой аргументы изменяются в интервалах ![]()
Оценим интеграл по модулю
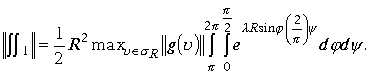
От элемента площади остался один модуль
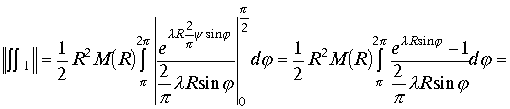
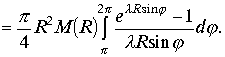
Заменим подынтегральную функцию ее максимальным значением в интервале интегрирования. Функция
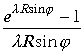 на концах интервала интегрирования неопределена .Раскроем эту неопределенность
на концах интервала интегрирования неопределена .Раскроем эту неопределенность
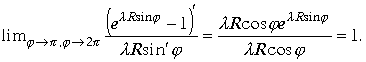
Эта величина является максимальной величиной функции в заданном интервале. Оценим величину функции в промежутках интервала интегрирования
Тогда
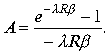 Для случая
Для случая 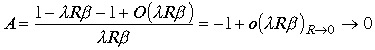 .
.
Если произведение
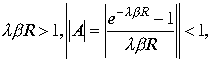
так как
Следовательно подынтегральная функция имеет максимальное значение равное единице. Поэтому интеграл
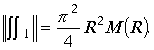 Если максимальное значение модуля функции
Если максимальное значение модуля функции
![]() то
то 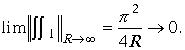
Доказано, что
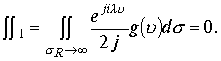
Все операции по первому интегралу переносятся во второй
![]()
Так, что
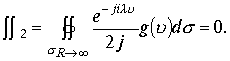
Следовательно интеграл для верхней полусферы
![]()
Проведем доказательство для изолированного направления в верхнем полупространстве. Интегралы
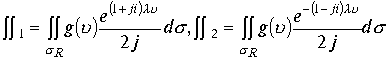 .
.
Для интервала
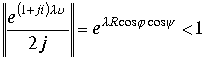 ,
,
для интервала
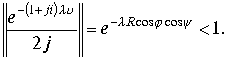
В верхней половине полусферы аргумент
![]() Оценка модуля интегралов
Оценка модуля интегралов ![]() сводятся к оценки выражений
сводятся к оценки выражений
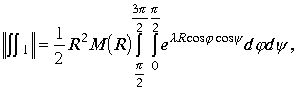
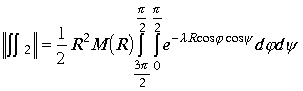 .
.
В пределах
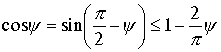 .Таким образом, для оценки интегралов необходимо рассмотреть интегралы
.Таким образом, для оценки интегралов необходимо рассмотреть интегралы
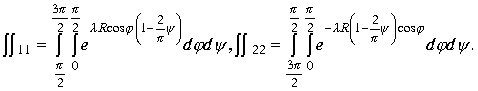
Преобразуем интегралы к повторным
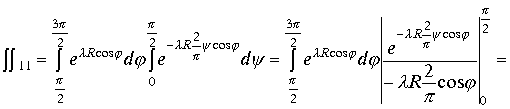
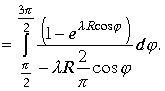
Второй интеграл дает выражение
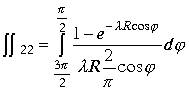 .
.
Подынтегральные выражения на концах интервала имеют неопределенность. Раскрывая неопределенность получим
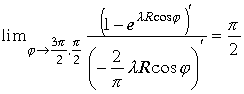 ,
,
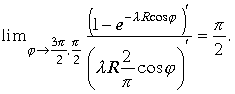
Подставляя эти оценки в исходные интегралы получим
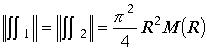 . Если максимальное значение
. Если максимальное значение
Функции ![]() то
то 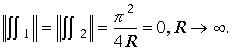 Таким образом , доказана вторая часть леммы. Сумма интегралов доставляет доказательство леммы К . Жордана в пространстве
Таким образом , доказана вторая часть леммы. Сумма интегралов доставляет доказательство леммы К . Жордана в пространстве ![]() .
.
![]()
Проекция интеграла на плоскость Z даст интеграл
![]() Если функция
Если функция ![]() соответствует условиям Леммы и содержит ограниченное число полюсов в верхнем полупространстве , то по теореме Коши для многосвязных областей имеет место равенство
соответствует условиям Леммы и содержит ограниченное число полюсов в верхнем полупространстве , то по теореме Коши для многосвязных областей имеет место равенство
![]()
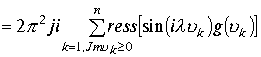
Но по лемме К. Жордана
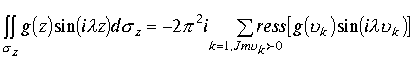 .
.
Пример .Вычислить интеграл
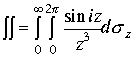 . Выберем вспомогательную функцию
. Выберем вспомогательную функцию 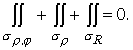 Подынтегральная функция не имеет особых точек в верхнем полупространстве. Кроме того ,
Подынтегральная функция не имеет особых точек в верхнем полупространстве. Кроме того ,![]() по лемме Жордана. Для вычисления интеграла
по лемме Жордана. Для вычисления интеграла ![]() ,рассмотрим Лорановское разложение функции синус в окрестности точки 0 и оценим подынтегральную функцию
,рассмотрим Лорановское разложение функции синус в окрестности точки 0 и оценим подынтегральную функцию 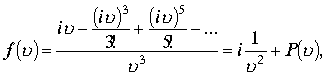
где
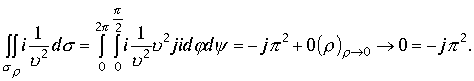
Проекция интеграла на плоскость Z равна
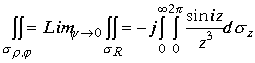 .Окончательно получим
.Окончательно получим
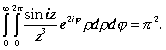 Преобразуем подынтегральное выражение. Введем
Преобразуем подынтегральное выражение. Введем ![]()
![]()
![]()
![]()
![]()
суммируя мнимую и действительную части получим
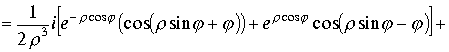
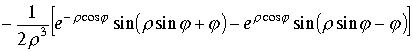 .
.
Отделяя действительную и мнимую часть в исходном интеграле получим :
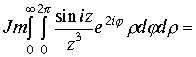
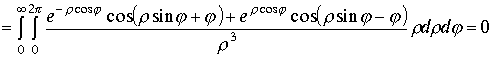
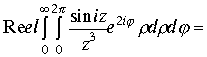
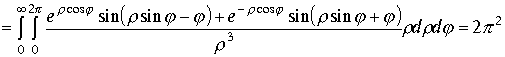 Пример 3. Продолжение исследования вычисления примеров 1,2 пункта 1.7.1. Вычислим интеграл примера 2 . Представим интеграл в виде суммы двух равных частей
Пример 3. Продолжение исследования вычисления примеров 1,2 пункта 1.7.1. Вычислим интеграл примера 2 . Представим интеграл в виде суммы двух равных частей
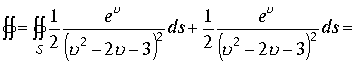
Знаменатели дроби выразим через произведение линейных множителей , на которые раскладывается квадратный трехчлен. На основании равенства
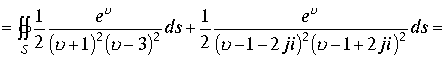
Если поверхность S , охватывает все изолированные точки, то применяя последовательно формулу Коши получим
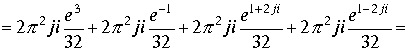
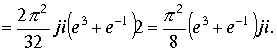
Совпадает с результатом расчета примера 2 пункта 1.7.1.
Вычислим интеграл по другому варианту. Разложение квадратного трехчлена на простейшие множители в пространстве позволяет квадрат этого трехчлена записать в виде произведения четырех множителей. Интеграл примет вид
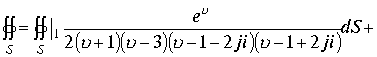
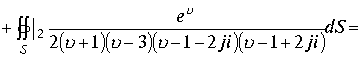
в этих выражениях каждый из интегралов содержит по четыре изолированные точки –полюса подынтегральной функции. Каждая из пространственных точек является полюсом второго порядка. Вычисление интеграла сводится к вычислению четырех интегралов . По теореме для многосвязных областей каждую изолированную пространственную точку окружим сферической поверхностью с радиусом стремящимся к нулю.
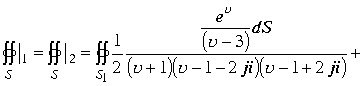
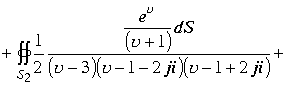
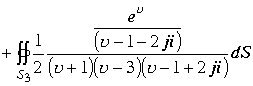
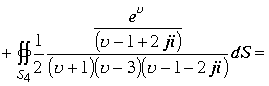
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com