 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
8.2. Квантовые числа кварков есть следствие многосвязности пространства.
Структура нейтрино электронного, мюонного, тау-нейтрино (частицы соответственно обозначаются
) определена в пространстве 
. Исследования этого комплекса проведены в главе 1. Комплекс в сферических координатах имеет в пространстве делителей нуля изолированное направление в виде 
, которое принимаем за лептонный заряд 
.Лептонных изолированных направлений может быть четыре: два имеют направление в верхнее пространство – полусферу 
, два в нижнее полупространство -полусферу
. Электронное нейтрино 
представляет замкнутое комплексное пространство мнимого радиуса. В координатном виде это можно написать в виде 
, где 
- коэффициент пространственной или энергетической характеристики частицы (в общем случае это комптоновская длина волны 
). На рис. 69, 70 даны модели электронного нейтрино с положительной +1 спиральностью, и отрицательной спиральностью-1 соответственно. Спиральность определяется тривиальном методом: поворот составляющей мнимого радиуса против или по часовой стрелки (относительно направления вертикальной оси) до совмещения ее начальной исходной точки до начальной точки вертикальной составляющей этого радиуса на минимальный угол 
.На рис 69, 70 повороты обозначены стрелочками.
Модели электронного нейтрино и антинейтрино отражают самое существенное в структуре этих частиц. Энергия, которая создает эти устойчивые структуры, распределяется в пространстве, создавая соответствующие изолированные направления лептонного заряда и спиральность.
Электронное антинейтрино
представлено на рис 71, 72. Антинейтрино может иметь два варианта отрицательного изолированного направления также в верхнее и нижнее полупространство и два значения спиральности 
. Соответственно электронное антинейтрино может быть выражено в координатном виде
.
Аннигиляция нейтрино и антинейтрино приводит к образованию двух гамма квантов. Согласно алгебре комплексных чисел имеем
. Возможны и другие варианты 
. Гамма–квант имеет действительный модуль. Направление гамма кванта определяется его коэффициентами 
и зависит от спиральности нейтрино и антинейтрино.
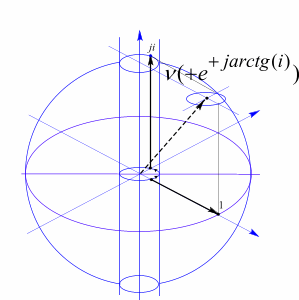
Рис 69 Модель электронного нейтрино с положительной спиральностью. Глюонное поле создает изолированное направление положительного лептонного заряда.
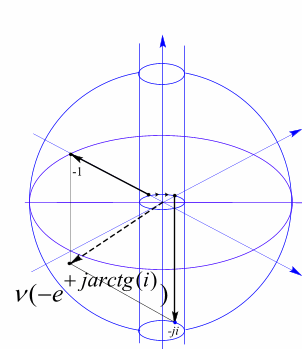
Рис. 70. Модель электронного нейтрино с отрицательной спиральностью.. Структура глюонного поля имеет изолированное положительного направления лептонного заряда.
Аннигиляция есть образование в нейтринном пространстве скомпенсированных лептонных 
- туннелей, которое приводит к росту многосвязности замкнутого пространства и увеличению его массы. Известные к настоящему времени массы таковы:
,
,
.
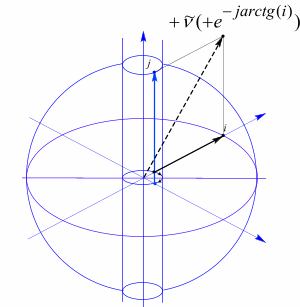
Рис 71 Модель электронного антинейтрино с положительной спиральностью. Лептонный заряд отрицателен.
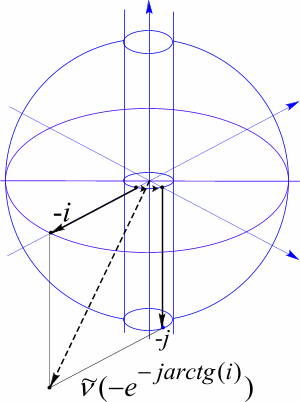
Рис72 Модель электронного антинейтрино с отрицательной спиральностью. Лептонный заряд отрицателен.
Увеличение массы частицы с одинаковыми свойствами есть следствие роста многосвязности пространства за счет возникновения скомпенсированных лептонных туннелей.
Модель мюонного нейтрино 
и мюонного антинейтрино
повторяет модель электронного 
нейтрино и антинейтрино 
с добавлением к ней скомпенсированного одного лептонного туннеля (фактически гамма кванта удерживаемого в замкнутом объеме частицы).
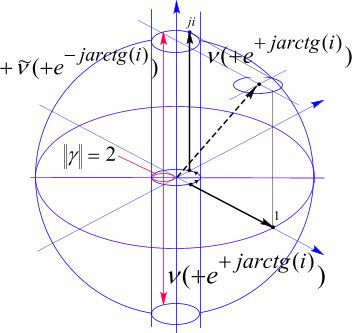
Рис. 73 Модель мюонного нейтрино. Скомпенсированный лептонный туннель определяет гамма квант с весовым коэффициентом равным
Скомпенсированный туннель имеет свои характеристики и в дальнейшем структура, включающая один такой туннель, получила название странного заряда –
S. На рис 73, 74 даны модели мюонного нейтрино. Мюонное нейтрино состоит из комбинации трех электронных нейтрино, две частицы из которых образуют скомпенсированный лептонный туннель. Чтобы не загромождать геометрические построения перейдем к изображению частиц через условное представление многосвязного пространства. На рис 75, 76 дано изображение частиц мюонных нейтрино взамен моделям на рис 73, 74. Модель электронного нейтрино и антинейтрино через многосвязность пространства представлены на рис 77, 78 в соответствии с рис 69, 70.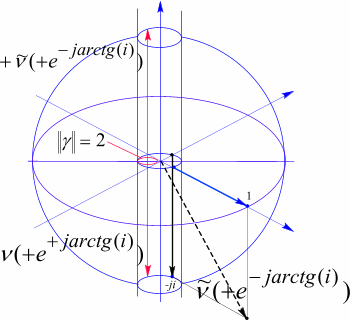
Рис. 74 Модель мюонного антинейтрино. Скомпенсированный лептонный туннель дает гамма квант с весовым коэффициентом
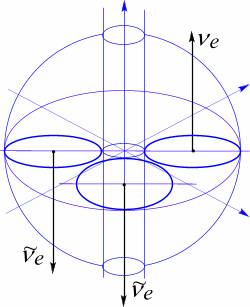
Рис 75. Связность пространства, характеризующее структуру мюонного антинейтрино.
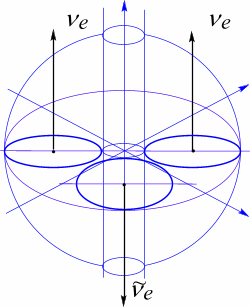
Рис. 76 Связность пространства, характеризующего мюонное нейтрино.
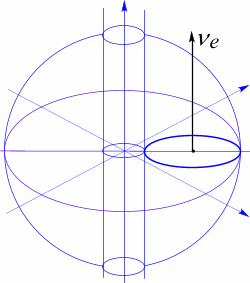
Рис 77. Связность пространства, характеризующая структуру нейтрино.
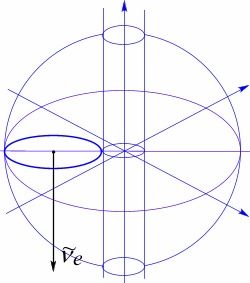
Рис 78. Связность пространства, характеризующее структуру антинейтрино.
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com