Продолжение 2 из 3. 8.9 Вычисление масс микрочастиц по кварковым композициям и модам распада. Вычисление квантовых чисел микрочастиц, исследование связи спина, изоспина, четности с величиной массы микрочастицы. Реализация квантовой СРТ-теоремы. Исследование закона не сохранения четности.

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

Продолжение 2 из 3. 8.9. Вычисление масс микрочастиц по кварковым композициям и модам распада. Вычисление квантовых чисел микрочастиц, исследование связи спина, изоспина, четности с величиной массы микрочастицы. Реализация квантовой СРТ-теоремы. Исследование закона не сохранения четности.

Аналогично имеем

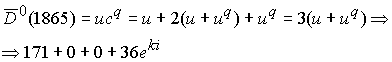
Такая комбинация глюонного поля дает массу частицы Мэв.

Расхождение составляет 35 %., так как имеем несоответствие с квантовыми числами частицы.

Глюонное поле частицы определим при замене кварка на кварк в одном из нейтральных пионов. Тогда суммарное глюонное поле будет отвечать квантовым числам частицы

.Вычисление массы дает величину

Мэв. Расхождение равно 9 %. Cпин равен нулю, так как весовой коэффициент глюонного поля равен нулю. Изоспин равен . Формула расчета дает точное соответствие экспериментальным данным.

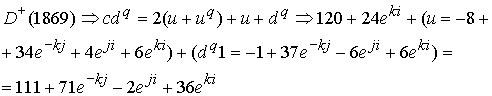
Это глюонное поле соответствует квантовым числам и дает массу микрочастицы

Мэв. Расхождение составляет 14,7 %. Глюонное поле имеет спиновую составляющую, удельный вес которой равен 0,099Мэв, и значительно ниже точности измерения массы самой частицы Мэв. Это дает основание не учитывать влияние этой величины. Изоспин равен

Если кварк заменить на кварк , получим . Вычисление массы микрочастицы дает величину Мэв. Расхождение составляет 2,2 %. Однако это барион по своим квантовым числам . Это резонанс . Расхождение для которых по массе составит соответственно .

Таким образом, вычисления показывают зависимость квантовых чисел микрочастиц и их масс от структуры глюонного поля и принадлежности этих частиц по классификации на мезоны, барионы и так далее.

Каоны.

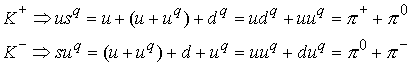
Кварковые композиции каонов при замене кварка S на кварк , дают следующие моды распада

в полном соответствии с экспериментальными модами распада.

Кварковые композиции дают выражения для суммарных глюонных полей. Для

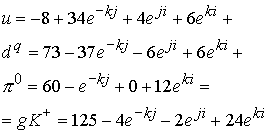
Этому глюонному полю соответствует масса частицы Мэв. Расхождение составляет 10,9 %.

Для имеем

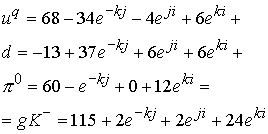
Это глюонное поле соответствует массе Мэв. Расхождение составляет 11,4 %. Расхождение между вычислениями масс отрицательного и положительного каона составляет 0,38 %.

Вычисления глюонных полей показывают, что если в кварках произвести замену знаков электрического и лептонного глюонного поля то есть применить теорему

. Эта операция произойдет внутри микрочастицы. В этом случае массы микрочастиц совпадут, та как глюонное поле будет выражаться для них одинакого.

Глюонное поле лептонного и электрического заряда малы. Поэтому величина изоспина зависит только от заряда кварка S, так что микрочастицы имеют квантовые числа .

Кварковая композиция нейтрального каона . Эта композиция дает 2-х пионную моду распада и трех пионную. Исследуем этот экспериментальный факт.

. Эта мода распада закреплена за

Глюонное поле равно . Вычисление массы дает величину Мэв. Расхождение с экспериментальной массой составляет 8,3 %.

При образовании нейтрального пиона глюонные поля лептонного и электрического заряда аннигелируют на величину глюонного поля равную

, что по массе составляет 177,65 Мэв. Величина превышающая массу нейтрального пиона. В связи сэтим поворот одновременно электрического и лептонного полей в нейтральном пионе вызовет изменение массы частицы и ее квантовых чисел до величин

. Глюонное поле будет равно

Это дает массу частицы равную 764,29 Мэв. Этой массе и квантовым числам отвечает

-мезон. При кварковой комбинации глюонное поле аннигилирует на величину

. Эта величина в микрочастице дает увеличение массы и превращение нейтрального пиона в другую частицу с глюонным полем

, которое дает массу 872, 66 Мэв. Эта величина и квантовые числа соответствуют частице .

Так как каон может иметь две такие коррекции, то его глюонное поле можно представить в виде , которая определяет массу

Мэв. Расхождение составляет 6,2 %.

Так как, величина энергии аннигиляции соизмерима с энергией нейтрального пиона, то при образовании нейтрального каона возможен вариант глюонного поля в виде

, что дает массу частицы Мэв. Расхождение составляет 1,5 %.

Квантовые числа этой частицы равны . В физике микрочастиц распад каона на два пиона и на три пиона вырос в проблему нарушения четности. Вычисления показывают, что это обычный процесс происходящий при взаимодействии полей при образовании микрочастиц.

Кварковая композиция положительного каона дает следующее выражение для вычисления глюонного поля микрочастицы , но по введенной системе , поэтому используя выражения для кварков из 9,5 будем иметь.

. Расчет массы для этого глюонного поля дает величину 586 Мэв, которая отличается от экспериментальной 494 Мэв на 18 %.

Глюонное поле положительного каона можно откорректировать за счет спина кварка заменив его на кварк

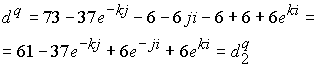
Тогда глюонное поле кварка выразится в виде

. Вычисление массы для этого глюонного поля дает величину 482,23 Мэв. Расхождение с экспериментальной массой составляет 2,4 %.

Изменение величины весового коэффициента возможно в следствии равенства масс единичного лептонного глюонного вихря разных зарядов.

Отрицательный каон имеет кварковую композицию

Глюонное поле через весовые коэффициенты выразится в виде

. Для этой композизиции глюонного поля масса микрочастицы равна 559,78 Мэв и отличается от экспериментальной массы на 13 %.

Здесь также возможна корректировка глюонного поля за счет спина кварка , заменив его кварком

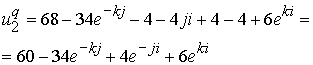При такой замене будем иметь глюонное поле , которое даст массу частицы 480,85 Мэв и расхождение с экспериментальной величиной 2,7 %.

Нейтральный каон имеет кварковую комбинацию Эта комбинация соответствует комбинации весовых коэффициентов двух нейтральных пионов (что соответствует и моде распада нейтрального каона

Таким образом, глюонное поле имеет вид ,вычисления по которому дают массу микрочастицы 558,71 Мэв, которая отличается от экспериментальной массы равной 498 Мэв на 12 %.

Возможен вариант рассмотрения глюонного поля нейтрального каона как полу суммы глюонных масс положительного и отрицательного каонов

, что соответствует массе 481,54 Мэв и расхождение составляет 4,3 %.

Из кварковой композиции микрочастицы имеем весовые коэффициенты глюонного поля и самого поля в виде

Имеем массу микрочастицы Мэв. Экспериментальная масса равна 547 Мэв.

Расхождение составляет 2,4 %.

Далее рассмотрим частицу кварковые композиции соответственно имеют вид На этой композиции проверяется введенная систематизация кварков, по которой , тогда подтверждаются экспериментальные моды распада частиц

а также второй вариант

Конкретные моды распада для этимх частиц не установлены. Энергетический расчет дает вариант Масса глюонного поля такого распада будет соответствовать Вычисление массы дает величину Мэв.

Аналогично обстоят дела и сдругими видами микрочастиц этой серии. Расхождение расчетов составляет от 8 до 14 %.

Система отвечает кварковой композиции микрочастицы с массой 3097 Мэв. Откорректированное глюонное поле по нейтральному пиону дает . Вычисления дают массу частицы Мэв против экспериментальной величины 3097 Мэв. Расхождение составляет 9,4 %.

Мезон с массой 9460 Мэв имеет кварковую композицию . Замена кварка (введено в классификацию кварков), дает глюонное поле в виде

. Вычисление массы кварка дает значение Мэв.

Моды распада частицы В не приводятся конкретно. Кварковая композиция показывает, что аннигиляция внутри системы создает поле частицы как . Так, что глюонное поле микрочастицы . Вычисление массы дает величину

Мэв. Экспериментальная масса равна 5279 Мэв. Расхождение составляет 2 %.

-Гиперон имеет кварковую композицию . Замена кварка его композицией дает кварковую композицию Гиперона, которая объясняет моду распада . Замена кварков на их комбинации из единичных глюонных полей и весовых коэффициентов дает выражение для суммарного глюонного поля гиперона

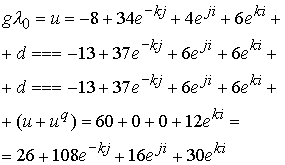
Это глюонное поле гиперона соответствует массе Мэв. Эта величина отличается от экспериментальной равной 1115,6 Мэв на 52 %. В связи с этим произведем две коррекции кварка на кварк повернув лептонную составляющую и кварка на кварк . В кварке были проведены повороты глюонных полей электрического и лептонного. В результате получаем выражение .

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com