 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
1.5. Изолированные особые точки в пространстве.
В пространстве
точка 
называется
изолированной особой точкой функции 
,если существует
окрестность 
этой точки, в которой 
аналитична,
кроме самой точки 
. Окрестность из круга в плоскости Z
превращается в
сферу . Если
существует конечный предел функции 
в точке , то точка
называется устранимой.
Вопрос об определении и классификации изолированных особых точек функции в пространстве оставляет без изменения теоремы, так как речь идет только о способе отыскания этих особых точек. Точка
называется полюсом функции 
, если 
.
Для изолированного направления 
существует
бесконечный делитель. Если
. Для того,
чтобы точка была полюсом функции 
необходимо и
достаточно, чтобы эта точка была нулем для
функции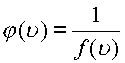 
.
Точка нуль в пространстве определяется еще одним
условием 
,
поэтому для изолированного направления функция 
должна
представлять произведение делителей нуля.
Бесконечность в пространстве представляется
также как произведение двух бесконечных
делителей 
.
Точка
называется полюсом порядка 
,
функции 
, если эта точка является нулем
порядка 
для
функции 
.
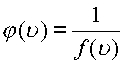При n=1 полюс называется
простым.
Если функция имеет порядок нуля равный
, то она
представима в виде
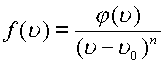, где
функция
аналитична в точке и 
.
Дробная функция или мероморфная не имеют других особенностей, кроме полюсов. Примером мероморфных функций остаются все целые функции и дробно-рациональные, тригонометрические функции и др. Алгебраическая комбинация мероморфных функций сумма, разность, произведение и частное двух мероморфных функций снова являются функцией мероморфной.
Мероморфная функция имеет конечное число полюсов. Разложение мероморфной функции в ряд имеет следующий вид
.
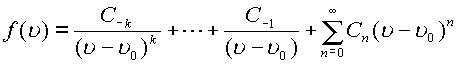Наибольший из показателей степеней у разностей
, стоящих
в знаменателе членов главной части ряда Лорана
совпадает с порядком полюса функции.
Если функция имеет бесконечное число членов главной части Лорановского разложения в окрестности точки, то эта точка считается устранимой особой точкой.
Существенно особой точкой считается точка, в которой функция не имеет предела ни конечного ни бесконечного.
Неравенство Коши.
Неравенство Коши остается в силе и в пространстве Y. Обозначим через М максимум функции
в области G пространства. Через R обозначим расстояние точки 
до границы
области. Тогда поверхность
сферической области
будет равна 
. Подставим в формулу
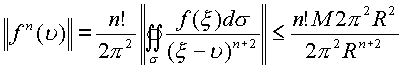. Откуда
получаем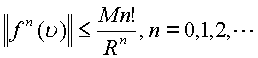
-конкретная
точка в области G. Следствием
этого неравенства являются две теоремы.
Теорема. Если функция 
аналитична во всем пространстве и
ограничена, то она постоянна.
Доказательство: Для первой
производной согласно формуле имеем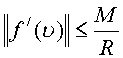 
.
По условию теоремы
M –ограничено, а при увеличении R модуль может быть сколь угодно мал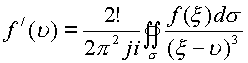
. Откуда следует,
что во всем пространстве 
.
Выразим это соотношение через двойной интеграл 
При рассмотрении двух точек
:
равных
соответственно 
, где 
-малое, подынтегральная функция
может быть представлена как разность двух дробей
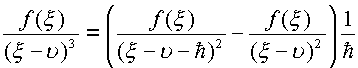, так что
интеграл выражается через разность двух
интегралов
.
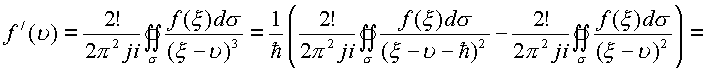
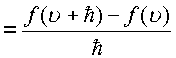Полученное выражение отвечает
формуле производной при стремлении 
,
которая равна нулю, поэтому 
. Что и
требовалось доказать.
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com