1.8.1. Понятия конформного отображения в пространстве

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

Теорема 7. Пусть функция W=f(n ) имеет в точке n ₀ производную f’(n ₀), отличную от нуля и от корней из нуля, то есть . Тогда эта функция реализует в точке конформные отображения. Это значит, что при переходе из пространства (n ) в пространство (W) касательная к любой гладкой кривой в фиксированной точке n ₀ поворачивается на один и тот же угол в пространстве и имеет один и тот же коэффициент растяжения.

Доказательство. Пусть в некоторой области пространства (n )

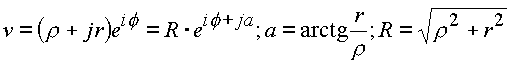
задана функция , дифференцируемая в точке n ₀ и (неравна корням из нуля).

Рассмотрим уравнение гладкой кривой g в пространстве в виде n =S(t), где t - параметр, меняющийся вдоль этой кривой, проходящий через точку . Проведем касательную к этой кривой в точке n ₀. Положение касательной в пространстве (ее наклоны к координатным плоскостям) характеризуется углами f ₀, y ₀.

Пусть g ’ – образ этой кривой, полученный при отображении ,

иными словами

Дифференцируем сложную функцию

по условию

тогда

обозначим . Пусть

Тогда из соотношения производной для сложной функции имеем

(1.67.)

Величину условимся называть комплексным углом поворота кривой g в точке n ₀ при отображении . Из формулы (1.64.) следует, что если то угол поворота в точке n ₀ не зависит от кривой и равен иначе говоря, все гладкие кривые, проходящие через точку n ₀ поворачиваются при отображении на один и тот же угол, равный аргументу производной в этой точке.

3амечание 1. Единственность касательной к гладкой пространственной кривой известна из дифференциальной геометрии.

Замечание 2. В случае, если то имеем дело с четырехмерным пространством, доказательство в котором аналогично.

Замечание 3. Постоянство коэффициента растяжения в точке доказывается стандартным образом как и в случае z-плоскости. Он равен .

Таким образом, здесь речь идет о подлинном отображении, конформном в трехмерном и более высокого числа измерений пространстве.

Рассмотрим теперь некоторые конкретные отображения.

А. Дробно-линейная функция

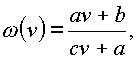(1.68.)

где a, b, c, a - комплексные пространственные переменные

при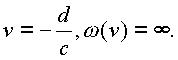

Если 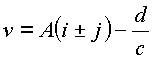, то

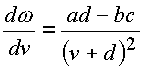
существует пр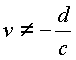и и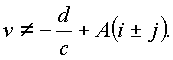

Уравнение однозначно разрешимо относительно n

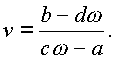
и функция определена в пространстве (w ).

В точке 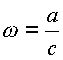функция равна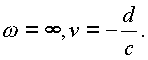 , а в точке ,

Таким образом, дробно-линейная функция осуществляет отображение пространства n на пространство w .

Функцию (1.65.) можно представить в виде

Рассмотрим отображение, которое является основой

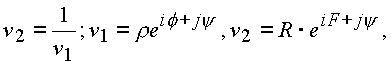
где r , f , y - действительные числа.

Тогда

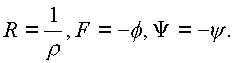
Если y - комплексное, то

где

Тогда и n ₂ будет иметь вид

Проведем преобразования

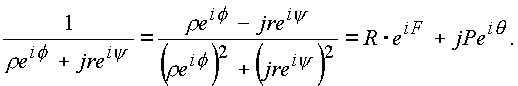
Знаменатель

где

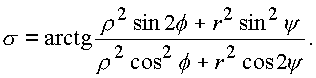
Таким образом,

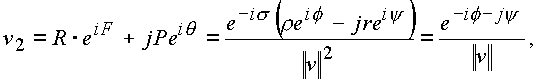
где y - комплексное.

Итак, если , то

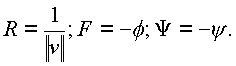
Таким образом лучи в пространстве (n ), идущие под углами f , y , поворачиваются и проходят под углами -f , -y .

Отображение обладает свойством инверсии (рис. 34.)

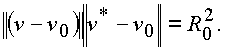
Для доказательства можно рассмотреть сечения плоскостями f =const и проекцию на плоскость (z).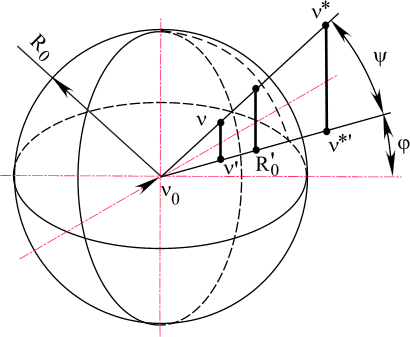

Рис. 34. Инверсия точек в комплексном пространстве.

В. Отображение шара в шар. Рассмотрим дробно-линейную функцию следующего вида:

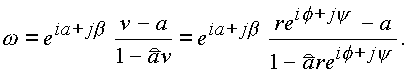(1.69.)

где a, b - действительные числа.

Если a=z+js , то

Рассмотрим "сечения":

a) b =0, y =0, a=a₁,

тогда

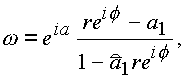
то есть имеем круг в соответствующем сечении;

б) при a=0, f =0, a=a₂, имеем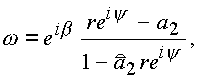

это снова круг.

Замечание. Аналогично тому, как это сделано в [7] для плоского случая, можно показать, что подмножество дробно-линейных преобразований дающих отображение шара на себя, является множеством движений пространства Лобачевского (если шар с выколотой осью назвать пространством Лобачевского).

Проведем выкладки, связанные с этим отображением, более детально:

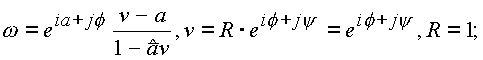
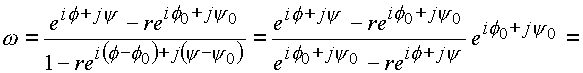
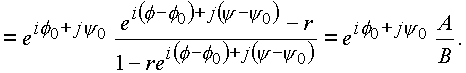
Распишем числитель этого выражения А

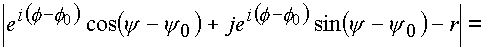
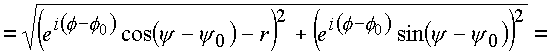
а также знаменатель B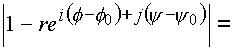

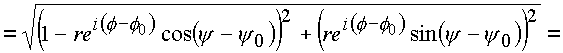
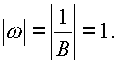
C. Отображение верхнего полупространства на единичный шар. Функция (рис. 35)

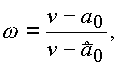
где

отображает верхнее полупространство на внутреннюю область, ограниченную единичной сферой, причем точка w переходит на плоскости в точку

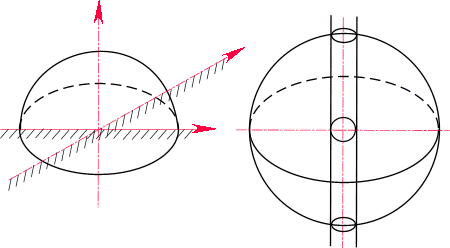
Рис. 35. Отображение верхнего полупространства в полное пространство

Доказательство. Достаточно показать, что всякая точка плоскости (z) переходит при указанном отображении на поверхность единичной сферы. В самом деле

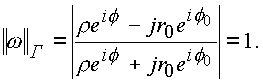
В общем виде отображение записывается в виде

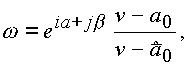
где a, b - любые действительные числа.

Д. Функция Жуковского.

Рассмотрим функцию

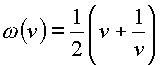(1.70.)

и определим области однолистности этого отображения в пространстве. Как обычно, положим

где r , f действительные числа; y - комплексное.

Предположим, что n ₁ и n ₂ переходят в одну точку в пространстве (w )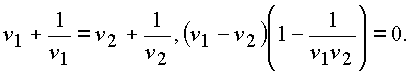

Таким образом, область однолистности пространства (n ) не должна содержать точек, связанных соотношением

В пространстве (n ) - это точки, лежащие внутри или вне сферы с выколотой осью.

Исследуем отображение при соблюдении этих ограничений

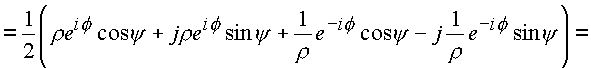
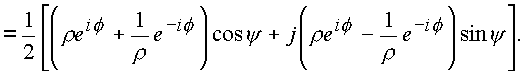
Проведем преобразование комплексных частей

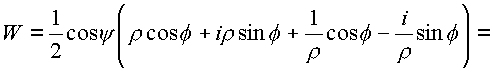
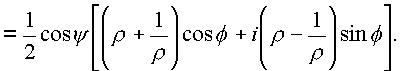
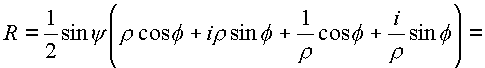
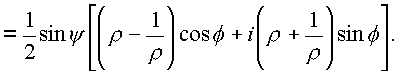
Применим формулу Эйлера:

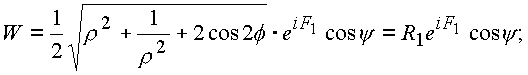
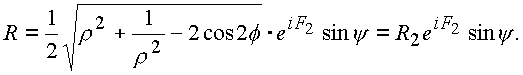
Проведем последовательно сечения сферы плоскостями, параллельными плоскости (z). Это плоскости y =const. Сначала положим y =0, тогда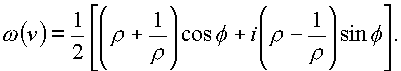

Это прежняя функция Жуковского в плоскости (z). На рис.36 представлено отображение, осуществляемое этой функцией. Поверхность сферы сжимается в круг с двойной границей, который по диаметру перерезает выколотая ось. Покажем, что кривые C₁, C₂, C₃, C_i при своем отображении не имеют точек пересечения в круге радиуса R=r получим комплекс

Преобразуем его по формуле Эйлера

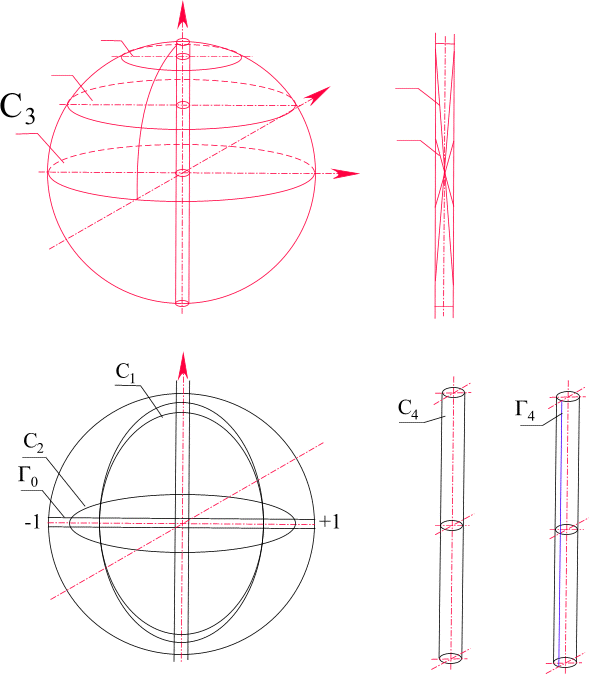
pic36.gif (30000 bytes) Рис. 36. Отображение внешнего пространства сферы в пространство круга радиуса, равного радиусу сферы толщиной.

Рис. 36. Отображение внешнего пространства сферы в пространство круга радиуса, равного радиусу сферы толщиной.

Если R₂=R₁, то одновременно должны выполняться два условия:

которые вытекали бы из равенства модулей комплексов. Но это не выполнимо. Аналогичная ситуация возникает, если предположить, что F₁=F₂ для этих кривых.

Таким образом, отображение плоскостей, секущих сферу, является однолистным. Выколотая ось также однозначно отображается в выколотую ось js .

Окружности радиуса корня из нуля отображаются в отрезки, дважды проходимые по линии Г₄ (рис. 36).

Е. Профили Жуковского в пространстве.

Рассмотрим в пространстве (n ) два касающихся изнутри в точке x=a шара (рис. 37). Функция Жуковского отображает поверхность большого шара на поверхность, напоминающую тело дельфина или фюзеляж самолета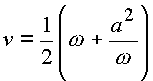

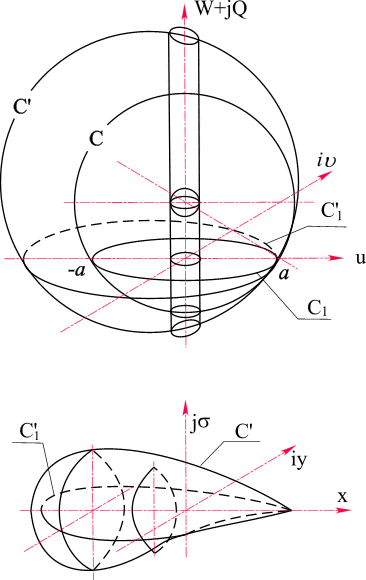
Рис. 37. Отображение пространства, заключенного между двумя сферами, в пространственный объем типа "Капля"

Плоскость Q=0 переводит функцию в z - плоскость, так что получаем отображение контура в контур С₁, также лежащей в z -плоскости.

Если рассматривать отображение плоскости, заданной углами f =0, f =p , то получим контур С. Система этих контуров и задает отображение (рис. 37).

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com