 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
1.7.2. Интеграл от рациональных функций.
Пусть
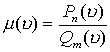, где 
и 
есть многочлены степени n и m соответственно
Сходимость интеграла от функции
обеспечивается соотношением степеней многочленов как 
. В соответствии с пространственной комплексной алгеброй многочлен знаменателя разложим на произведение квадратных трехчленов, как минимальных по степени многочленов, содержащих два вида корней: два корня в плоскости (z) два корня в пространстве (
.
При вычислении интегралов в пространстве необходимо соблюдать условия , которые обеспечивают эквивалентные разложения подынтегральной функции в области ее определения. Нахождение критических точек в пространстве зависит от области определения функции и возможности ее разложения на эквивалентные разложения. Например, если функция определена в полном пространстве , то можно не использовать эквивалентные разложения. Если
функция определена только в верхнем или только в нижнем полупространстве то нет условий для эквивалентных разложений. В первом случае условия есть , но ими можно не пользоваться, во втором случае их вообще нельзя применить. Если из полного пространства вычтена плоскость Z, то критические точки определяются из условия существования делителей нуля. Возможно существование областей, в которых содержатся не все критические точки , характеризующие эквивалентные разложения.Пример
Корни
и 
лежат в плоскости (z),корни 
и
лежат в пространстве (
рис 32.
Многочлен разлагается на множители по двум вариантам
Второй вариант разложения в комплексном пространстве представим в виде
Разложение представлено произведением двух комплексных пространственных чисел. Радиусы этих чисел представлены корнем квадратным из исходного многочлена. Аргументы комплексов представлены функцией
arctg от одинаковых комплексов. Если переменная u =1, то произведение состоит из двух множителей, модуль каждого из которых равен 2,а аргумент соответственно
.Если переменная u
равна соответственно корням многочлена u
=-1 или u
=3 то множители превращаются в делителей нуля.
Этот пример показывает, что изолированная ось делителей нуля смещается в точку
.На изолированной оси в пространстве 
находятся пространственные корни многочлена u
3 и u
4,а также и точки u
1 и u
2.
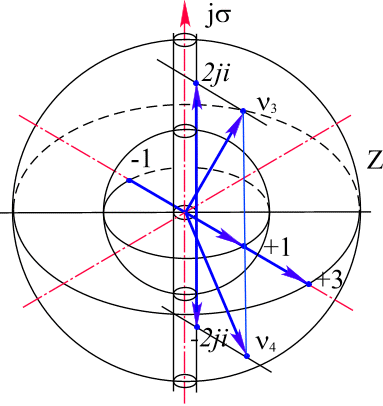
Рис. 32. Особые точки в пространстве
Пример
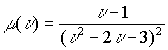
Разложим функцию
на дроби в пространстве
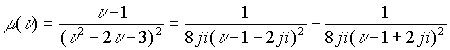
В пространстве нуль доставляется как произведением делителей нуля так и конкретно нулем. Поэтому при разложении по второму варианту в пространстве точки
и 
дают нуль как произведение делителей и критические точки располагаются на изолированной оси. Это подтверждает разложение 
на сумму дробей. В знаменателе этого разложения нуль есть при 
и 
. При 
и 
знаменатели дробей не превращаются в нуль, поэтому рассматриваются эти точки как критические точки на изолированной оси. В этом случае имеем нуль как произведение делителей нуля.
Функция
не регулярна в пространственных точках 
,которые являются пространственными корнями квадратного трехчлена в соответствии с примером.
Изолирование точек
и
в пространстве происходит при окружении точек сферой 
, радиус которой стремится к нулю
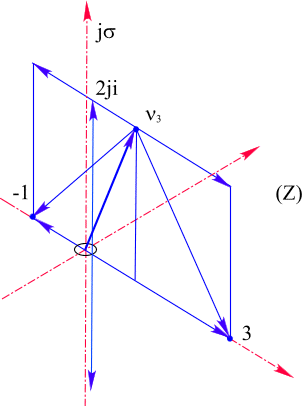
Рис. 33. Эквивалентность особых точек из плоскости
Z в пространстве Y.В пространстве в соответствии с ее геометрией любая точка может быть окружена сферой из делителей нуля
Радиус
R становится коэффициентом при сфере радиуса
, аргументы 
и 
при этом в зависимости от знака изолированного направления 
описывает верхнюю или нижнюю половину сферы.Сфера из точек делителей нуля около точки 
, лежащей в верхней части полупространства состоит из двух полусфер. Нижняя полусфера делителей нуля определяется изоляцией точки 
из плоскости Z,верхняя полусфера определяется сферой делителей нуля изолированной точки 
, лежащей также в плоскости Z с поворотом по углу
.
В нижнем полупространстве сфера из делителей нуля около точки
образуется также из двух полусфер:верхняя полусфера образуется выделением точки 
,нижняя полусфера выделением точки 
с поворотом по углу на .
Если точка
окружена сферой делителей нуля то при стремлении 
,
,
то двигаясь по изолированному направлению получим точку 
.
Аналогично, если
,
,
то имеем:
Таким образом поверхность составленная из точек делителей нуля около пространственных точек, в которых функция теряет аналитичность стягивается в поверхность сферы
внутри изолированной оси и происходит пространственная изоляция точек из плоскости Z . (рис 33)
Пример
где 
. Вычислим интеграл 
.
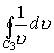Определим
.Подставляя в интеграл получим
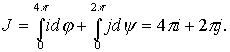Пределы интегрирования расставлены в соответствии с элементарной кривой 
в пространстве.
Пример
Вычислим интеграл
Элементарная площадка
. Подставляя в интеграл выражение функции и элементарной площадки получим
.
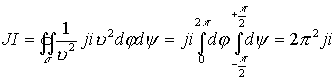Пределы интегрирования взяты из условия, что замкнутая поверхность
натянута без точек
Самопересечения на пространственную кривую
. Однако в сферических координатах необходимо ввести систему отсчета углов и по поверхности сферы 
,без учета поверхности изолированной оси. В этом случае интеграл JJ будет вычисляться в следующих пределах
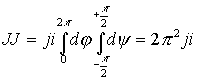
Расстановка пределов интегрирования определяется аргументом
,так как он в зависимости от рассматриваемого пространства может быть действительным и комплексным в соответствии с (1.42)
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com