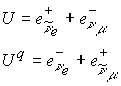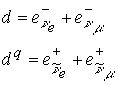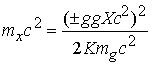 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
8.5. Структура глюонного поля. Расчет масс микрочастиц.
ОСНОВНЫЕ ПОЛОЖЕНИЯ.
В предыдущих главах разработаны, обоснованы и нашли экспериментальное подтверждение следующие основные положения, которые позволяют исследовать структуру глюонного поля микрочастиц.
Кварки
s, c, b, t представляют линейную комбинацию первых двух кварков и поэтому не могут претендовать на роль фундаментальных частиц. Эта линейная комбинация может быть продолжена без математических ограничений с предсказанием новых кварков. Через кварки u, d, s, t определены кварковые комбинации всех мезонов и барионов. Лептоны также определяются через кварковую комбинацию первых двух кварков. В основе всех комбинаций находится один принцип роста много связности комплексного пространства. Этот принцип частично отражен в принципе Паули. Исследование мод распада микрочастиц показало, что сумма кварковых комбинаций продуктов распада в точности равна исходной кварковой комбинации микрочастицы (без учета энергии распада).Кварки определены через электрически лептонные сопряжения зарядов
|
|
(8.1) |
Эти сопряжения получены после установления фундаментального свойства заряда быть положительным и отрицательным. Электрический, лептонный, гравитационный заряд есть изолированные направления в комплексном пространстве.
Предельное равенство
|
|
(8.2) |
дает абсолютную величину заряда
e через взаимодействие двух фундаментальных масс
Взаимодействие двух и более фундаментальных масс есть дефект этих масс, который соответствует массе частицы
|
|
(8.3) |
где К –количество пар взаимодействующий фундаментальных масс,
-энергия глюонного поля микрочастицы.
Зная массу микрочастицы можно рассчитать ее глюонное поле
|
|
(8.4) |
Расчет величины глюонного поля проверен неоднократно при выводе энергии связи атомных ядер, при расчете радиоактивных распадов. Формула выведена из структуры преобразований Лоренца.
Масса микрочастицы может быть рассчитана из формулы
|
|
(8,5) |
Формула определяет массу частицы и античастицы.
Масса микрочастицы
есть потенциал взаимодействия фундаментальных масс 
на расстоянии комплексной комптоновской длины волны 
микрочастицы. Потенциал есть в свою очередь дефект масс взаимодействующих фундаментальных масс, который есть следствие наличия глюонного поля в пространстве взаимодействия. Энергия глюонного поля обуславливает уменьшение суммарной исходной массы взаимодействующих частиц (схема аналогична ядерной материи). Пространственно временная метрика также дает пространственно- временной дефект, обусловленный наличием временной координаты
.
При переходе к энергетической массово-полевой метрике пространственная составляющая заменяется суммарной исходной массой фундаментальных частиц, временная составляющая массой глюонного поля, дефект пространственно – временной метрики есть масса микрочастицы.
Таким образом, потенциал взаимодействия фундаментальных масс на расстоянии комптоновской длины волны микрочастицы одновременно является дефектом пространственной энергетической решетки, обусловленном наличием глюонного поля и является массой микрочастицы. Глюонное поле в этом смысле присутствует в любом замкнутом пространстве. Свободного пространства нет, как нет пространства без материи. Изменение величины глюонного поля вызывает изменение массы микрочастицы или ее пространственной структуры. Глюонное поле требует определенного зарядового сопряжения комплексного пространства, фиксированного расположения взаимодействующих масс. Фундаментальное свойство заряда бать отрицательным, положительным и нейтральным есть свойство структуры пространства взаимодействия.
Таким образом, пространственно-временной континуум адекватен энергетическому массово – полевому континууму.
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com