 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
ГЛАВА 2. ПОДСЧЕТ ПОДЪЕМНОЙ СИЛЫ, ДЕЙСТВУЮЩЕЙ НА ТЕЛО КОНЕЧНЫХ РАЗМЕРОВ В ПОТОКЕ СПЛОШНОЙ СРЕДЫ
Классическая задача Н.Е. Жуковского о подсчете вектора подъемной сипы, действующей на тело конечных размеров в потоке сплошной среды, с применением методов теории функций пространственного комплексного переменного имеет принципиально новое решение, Решение проведем так
, чтобы показать непрерывность математического перехода от решения в z-плоскости к пространственному (Y). Покажем, что решение в пространстве содержит решение в плоскости как частный случай.Летящее тело в пространстве рассматриваем как изолированную особую точку. Пространственный поток для тела выступает как поле его взаимодействия, имеющее более высокий порядок по размерности.
2.1. Методика классического решения в Z-плоскости
Классическая формула C.A. Чаплыгина (1910 год) получена для подсчета подъемной силы, действующей на цилиндрическое тело в плоскопараллельном потоке. Вектор, сопряженный по
i-му вектору подъемной силы, выражается в виде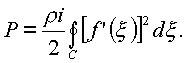
Решение относится к дозвуковым скоростям, следовательно скорость u
, плотность потока r связаны уравнением Бернулли-Эйлера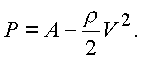 |
(2.1.) |
В плоскости комплексного переменного комплексный потенциал, описывающий плоский поток, обтекающий окружность радиуса
R, получается наложением циркуляционного потока [7]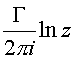 на
бесциркуляционный поток
на
бесциркуляционный поток
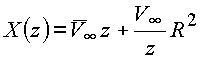 ,
,
где
Окончательное решение доставляется потенциалом
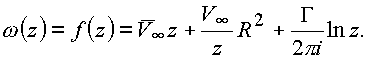
Бесциркуляционный поток получен, как результат наложения на функцию Жуковского реализующую отображения внешности круга
Этим приемом, оставаясь в рамках идеальной жидкости, Н.Е. Жуковский описал обтекание тела реальной жидкостью с трением. В зависимости от величины циркуляции при обтекании цилиндра возможны различные случаи нарушения симметрии потока относительно одной из осей координат. В силу этого главный вектор давления жидкости отличен от нуля, так как в слоях жидкости под цилиндром скорости бесциркуляционного потока обтекания цилиндра и чисто циркуляционного потока вокруг цилиндра складываются, а над цилиндром вычитаются.
С помощью дополнительного допущения Н.Е. Жуковский и С.А. Чаплыгин теоретически определили величину присоединенного вихря, выдвинув постулат о конечности скорости на задней острой кромке крылового профиля.
Величина циркуляции согласно классическим исследованиям определяется через критические точки потока. Для этого модуль производной комплексного потенциала
![]()
для точек, лежащих на цилиндре
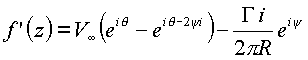 ,
,
для простоты полагают
q =0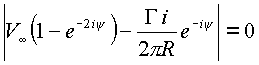
откуда циркуляция (с учетом угла
q ) равна![]() .
.
При пространственном обтекании крыла конечного размаха присоединенный вихрь согласно классической теореме Гельмгольца должен приходить и уходить в бесконечность Согласно второй теореме Гельмгольца направление вихря должно быть перпендикулярным плоскости вихря.
Решение в комплексной плоскости содержит такое исправление, которое одновременно удовлетворяет обеим теоремам Гельмгольца. Это направление функции
arctg в изолированной точке i которое до сих пор остается незамеченным, хотя оно несет в себе всю топологию обтекания.Исходя из этого нового физического условия, определим величину циркуляции
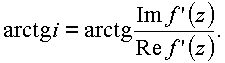
Для выполнения этого условия необходимо найти решение уравнения.
![]()
Положим
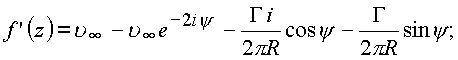
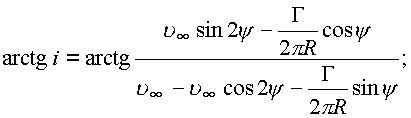
откуда величина циркуляции будет равна
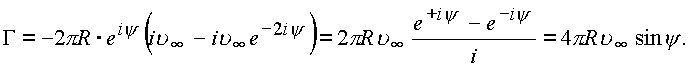
Таким образом, применив формулу гиперболического синуса, получили прежнюю формулу для величины циркуляции.
Новое физическое условие по определению величины циркуляции объясняет схему несущей линии Прандтля.
Сущность схемы крыла конечного размаха заключается в следующем: присоединенный вихрь крыла заменяют несущей линией вихря (с направлением
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com