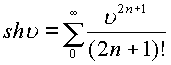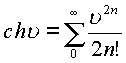|
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
1.4.1. Теорема Н. Абеля.
Если степенной ряд
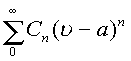 сходится в точке
сходится в точке Понятие области сферы в пространстве
 В силу
сходимости в точке
В силу
сходимости в точке ![]() член
член ![]() ограничен по модулю
ограничен по модулю ![]() и стремится к
нулю. Кроме того
и стремится к
нулю. Кроме того
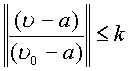 и
следовательно для всех n имеем
и
следовательно для всех n имеем
![]() .Откуда
вытекает равномерная сходимость на сфере
.Откуда
вытекает равномерная сходимость на сфере ![]() . Так как, K может быть сколь угодно близким к 1,
то имеем
. Так как, K может быть сколь угодно близким к 1,
то имеем ![]() .Из
теоремы Абеля, перенесенной в пространство
.Из
теоремы Абеля, перенесенной в пространство ![]() следует,
что областью сходимости степенного ряда
следует,
что областью сходимости степенного ряда 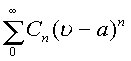 является сфера
с центром в точке
является сфера
с центром в точке ![]() радиуса R, равного
радиусу сходимости ряда.
радиуса R, равного
радиусу сходимости ряда.
Радиус сходимости определяется по формуле 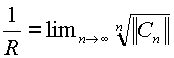 .
Следовательно ряд будет сходиться в области
сферы
.
Следовательно ряд будет сходиться в области
сферы![]() в
пространстве
в
пространстве ![]() . Это верхняя граница
сходимости.
. Это верхняя граница
сходимости.
Нижняя граница сходимости определяется как ![]() . Для
изолированного направления
. Для
изолированного направления
Область сходимости будет определяться как ![]() . Радиус
сходимости становится коэффициентом перед
делителем нуля. Нижняя граница
. Радиус
сходимости становится коэффициентом перед
делителем нуля. Нижняя граница ![]() .
.
При разложении
функции в ряд по степеням![]()
Справедливо следующее утверждение
: Однозначная аналитическая функция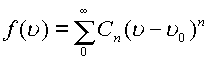 , где
коэффициенты ряда
, где
коэффициенты ряда ![]() определяются формулами
определяются формулами
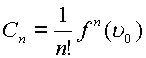 или
или
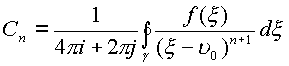 , кривая
, кривая ![]() натянута на сферу радиуса
натянута на сферу радиуса ![]() , которая имеет
центром точку
, которая имеет
центром точку ![]() и целиком лежит в окрестности этой
точки. Радиус сферы сходимости определяется
расстоянием от точки
и целиком лежит в окрестности этой
точки. Радиус сферы сходимости определяется
расстоянием от точки ![]() до ближайшей особой точки функции
до ближайшей особой точки функции ![]() в пространстве
в пространстве
![]() , либо до ближайшей особой точки,
расположенной на изолированной оси. Остаются в
пространстве
, либо до ближайшей особой точки,
расположенной на изолированной оси. Остаются в
пространстве![]() справедливыми следующие разложения
элементарных функций классического анализа
справедливыми следующие разложения
элементарных функций классического анализа
в точке![]() .
.
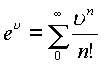 , ,
|
(1.58.) |
Эти соотношения имеют место во всем комплексном пространстве
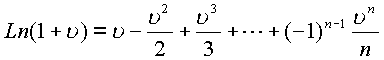
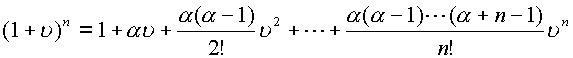 |
(1.59.) |
,в частности при
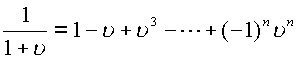 .Радиус
сходимости этих функций равен 1. Ближайшими
особыми точками для них служат
.Радиус
сходимости этих функций равен 1. Ближайшими
особыми точками для них служат ![]() , а также точка
, а также точка ![]() . Функции
. Функции ![]() и др.,
представленные сходящимся степенным рядом во
всем пространстве
и др.,
представленные сходящимся степенным рядом во
всем пространстве![]() , будут называться целыми
функциями.
, будут называться целыми
функциями.
Сумма, разность и произведение целых функций дают целые функции. Это свойство широко используется при разложении в степенные ряды.
Рассмотрим ряд примеров. Функция ![]() представляется
степенным рядом
представляется
степенным рядом 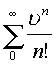 ,сходящимся во всем пространстве
,сходящимся во всем пространстве ![]() .Рассмотрим
сходимость ряда на конусе делителей нуля (или на
изолированной оси). Определим
.Рассмотрим
сходимость ряда на конусе делителей нуля (или на
изолированной оси). Определим ![]() и
воспользуемся формулой возведения делителей
нуля в целую степень n, согласно
таблице
и
воспользуемся формулой возведения делителей
нуля в целую степень n, согласно
таблице ![]()
Подставим данные соотношения в исходный ряд
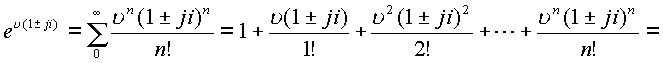
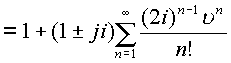 .
Коэффициент
.
Коэффициент 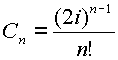 определяет радиус сходимости ряда
по изолированной оси и определяет расстояние от
нуля до особой точки на этой оси.
определяет радиус сходимости ряда
по изолированной оси и определяет расстояние от
нуля до особой точки на этой оси.
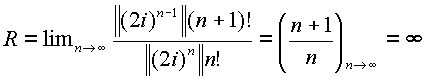 .
.
Таким образом, в области определяемой делителями нуля, ряд также имеет бесконечный радиус сходимости. Если
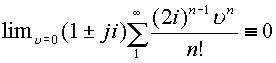 ,
естественно, что в этих выражениях
,
естественно, что в этих выражениях ![]() рассматривается
без делителей нуля.
рассматривается
без делителей нуля.
Далее имеем ![]()
![]() Складывая
и вычитая эти два равенства получим
Складывая
и вычитая эти два равенства получим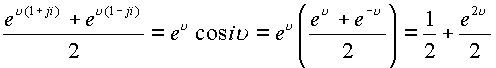
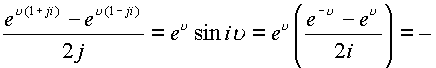
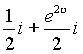
Учитывая, что функция
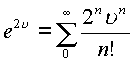 получим
получим 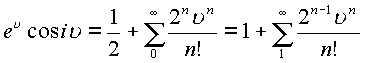
Таким образом, получено выражение для первой комплексной части при разложении функции
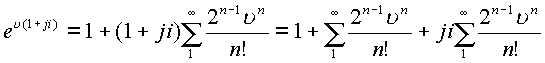 в ряд по
изолированному направлению. Вторая комплексная
часть получается аналогичным образом
в ряд по
изолированному направлению. Вторая комплексная
часть получается аналогичным образом
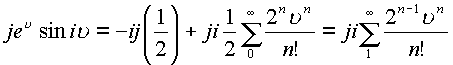
В комплексной плоскости
Z разложение функции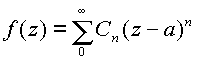 в круге сходимости радиуса R ( то есть для всех точек этого круга).
Центр окружности Г круга сходимости находится в
точке
в круге сходимости радиуса R ( то есть для всех точек этого круга).
Центр окружности Г круга сходимости находится в
точке 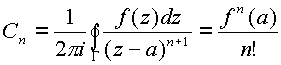 , где n =0,1,2,
….В пространстве
, где n =0,1,2,
….В пространстве 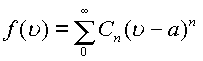 Однако необходимо подчеркнуть еще
раз, в сфере сходимости из точки
Однако необходимо подчеркнуть еще
раз, в сфере сходимости из точки 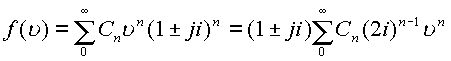 Радиус
сходимости этого ряда определяется из
соотношения
Радиус
сходимости этого ряда определяется из
соотношения 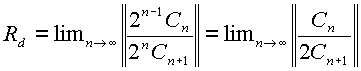 . В пределах этого радиуса точка
. В пределах этого радиуса точка ![]() .
.
При разложении в ряд Тейлора функции
![]() .
Рассмотрим ряд характерных примеров.
.
Рассмотрим ряд характерных примеров.
Пример. Рассмотрим разложение логарифмической функции на конусе делителей нуля. Согласно имеем
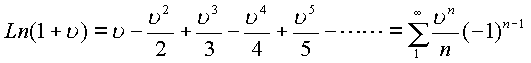
Известно, что ряд сходится в области сферы радиуса
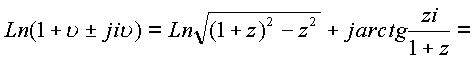
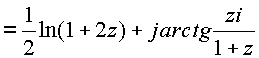 . Замена переменных
. Замена переменных ![]() на z сделана на основании свойства
изолированного аргумента. Подставим
на z сделана на основании свойства
изолированного аргумента. Подставим ![]() в правую часть
получим
в правую часть
получим
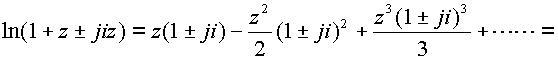
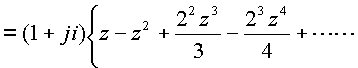 Если
Если ![]() , ряд
сходится и имеет радиус сходимости равный
, ряд
сходится и имеет радиус сходимости равный 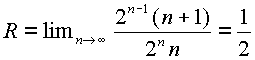 . Приравнивая
комплексные части с левой и правой стороны
получим
. Приравнивая
комплексные части с левой и правой стороны
получим
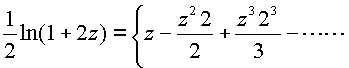
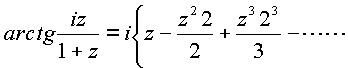
Таким образом, чтобы не было противоречий в разложении исходной функции как единого пространственного комплекса необходимо доказать, что вторая комплексная часть в левой стороне равна первой, а именно в комплексной плоскости имеем
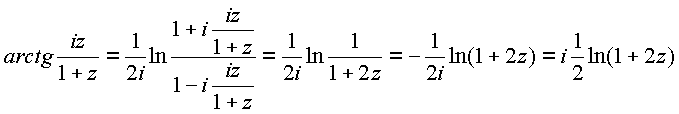 , что и требовалось доказать.
Одновременно получено следующее соотношение
, что и требовалось доказать.
Одновременно получено следующее соотношение
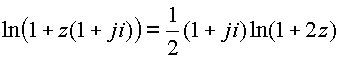
Пример.
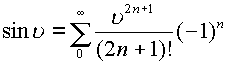 , ряд
сходится во всем пространстве
, ряд
сходится во всем пространстве ![]() .
Исследуем сходимость ряда в подпространстве
делителей нуля. Заменим
.
Исследуем сходимость ряда в подпространстве
делителей нуля. Заменим ![]() в левой и правой частях равенства
в левой и правой частях равенства
![]() , так как
функция
, так как
функция ![]() есть
четная функция и
есть
четная функция и![]() . Первая комплексная часть
равна
. Первая комплексная часть
равна
![]() .
Произведем замену
.
Произведем замену
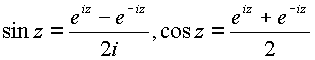 , получим
, получим
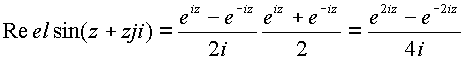
Разлогая в ряд экспоненциальные функции получим
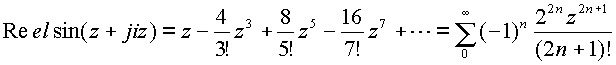 , радиус
сходимости этого ряда равен
, радиус
сходимости этого ряда равен
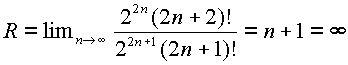 . Область
сходимости по изолированному направлению равна
бесконечности.
. Область
сходимости по изолированному направлению равна
бесконечности.
Пример. Ряд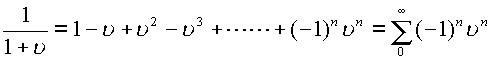 имеет радиус сходимости сферы
имеет радиус сходимости сферы ![]() . По
изолированному направлению ряд запишется в виде
. По
изолированному направлению ряд запишется в виде
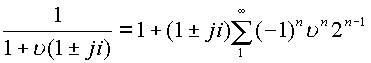 , радиус
сходимости этого ряда равен
, радиус
сходимости этого ряда равен 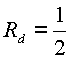 .
.
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com
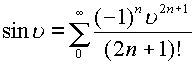 ,
,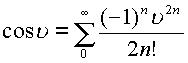 ,
,