1.3.6. Поверхностные интегралы

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

Рассмотрим в пространстве поверхность, которая охватывает объем, и сформулируем условия существования поверхностного интеграла.

Разобьем произвольную поверхность в пространстве на элементарные площадки ds , образованные пересечением кривых C_*, C^*. Сетку из кривых определим, анализируя дифференциалы.

Рассмотрим

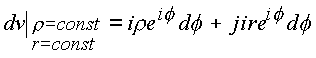
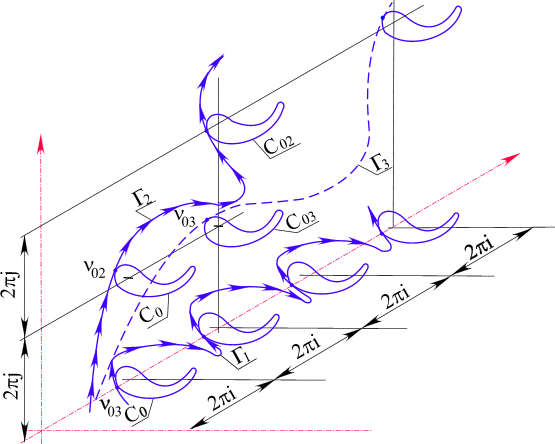
Рис. 28. Различные варианты однозначных ветвей логарифмической функции

Элемент площадки ds * образуется пересечением

Имеем

Поверхность ds состоит из четырех поверхностей

На рис. 28 дана геометрическая взаимосвязь площадок.

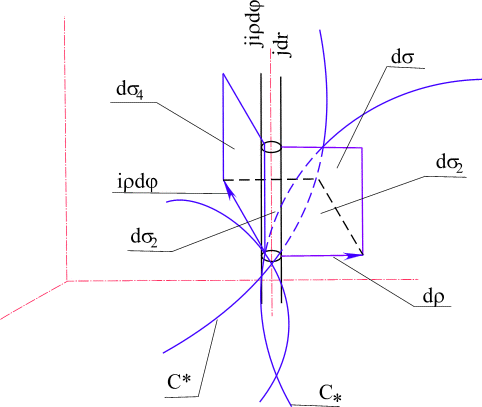
Рис. 29. Расположение элементарных площадок в комплексном пространстве.

Элемент ds * состоит из суммы проекционных площадок, одна из которых ds ₂ взята с отрицательным знаком, так как согласно геометрической интерпретации (рис. 29) эта площадка дважды входит в элемент: один раз в площадку. ds ₄ и один раз в площадку ds ₃.

Определим поверхностный интеграл

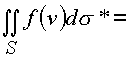
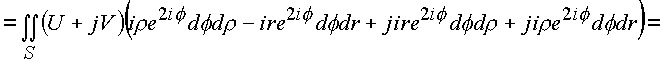
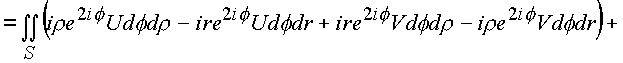
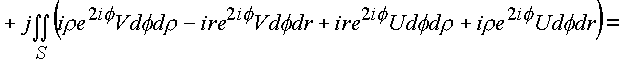
рассмотрим последовательно интегралы JJ₁ и JJ₂: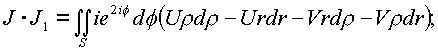

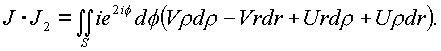
Преобразуем интегралы ll₁ и ll₂ в повторные интегралы по сеткам C^*, C_*: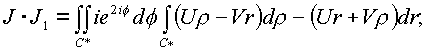

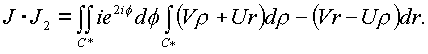
Криволинейные интегралы по C_* сведем к поверхностным, применив формулу Грина: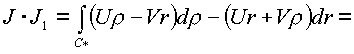

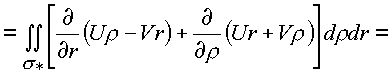
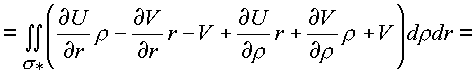
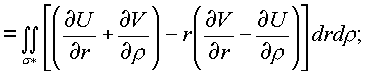
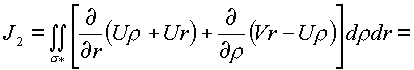
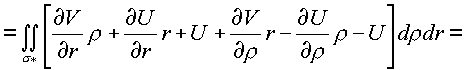
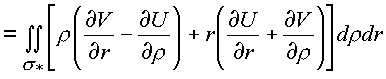
В результате преобразований имеем

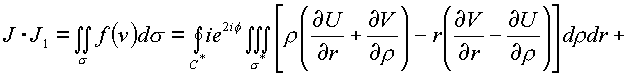
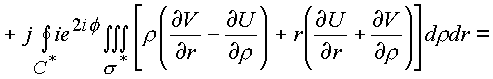
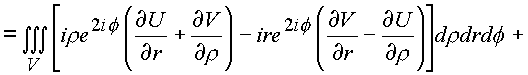
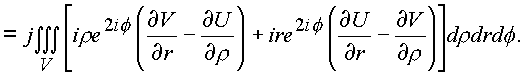
Подынтегральное выражение преобразуется к следующему виду объемного интеграла

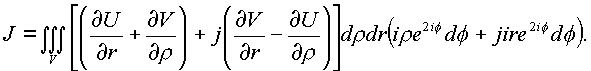
Подынтегральное выражение этого интеграла было получено на контуре f = const при исследовании криволинейного интеграла, когда по формуле Грина делался переход к поверхностному интегралу, поэтому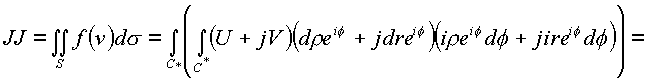

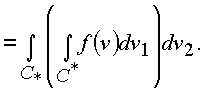(1.55.)

В итоге поверхностный интеграл по элементарной площадке свели к двукратному интегрированию сначала по кривой С*, а затем по кривой С_*.

Вследствие этого, если кривая является замкнутой кривой С₃, то поверхностный интеграл не зависит от формы поверхности, которая натянута в пространстве на эту кривую.

От поверхности натянутой на кривую С₃ (рис. 26), можно непрерывным образом перейти к поверхности , натянутой на кривую , окружающую изолированную точку n ₀.

Теорема 4. Пусть функция f(n ) дифференцируема в односвязной области G пространства (n ) и пусть имеется гладкая поверхность s . Тогда для любой точки n ₀, лежащей внутри объема G, заключенного внутри замкнутой (геометрически) поверхности, имеет место формула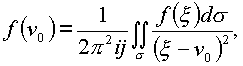

(1.56.)

где ds - дифференциал упомянутой поверхности.

Доказательство начнем со следующего замечания. Если около точки n ₀ построена шаровая поверхность (в нашем случае сфера с проколотыми вершинами)

то в этом случае

Поэтому

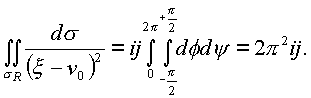(1.57.)

Далее. Функция 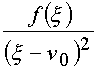дифференцируема по x в области пространства (n ) с выколотым туннелем, проходящим через точку n ₀. Выберем величину так, чтобы шар вместе со своей поверхностью лежал внутри поверхности s . Тогда интеграл преобразуется к следующему виду:

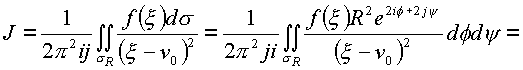
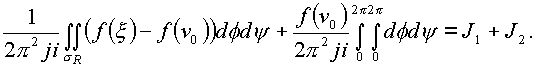
Рассмотрим обозначенные интегралы J₁ и J₂. Вычислим их.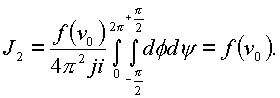

Докажем, что J₁=0. Радиус R можно взять сколь угодно малым. Поэтому в силу независимости интеграла от формы поверхности на основании формулы (1.55) и непрерывности функции f(n ) в точке n ₀ для любого e >0 найдется такое , что неравенство будет выполнятся для всех x , для которых

Отсюда

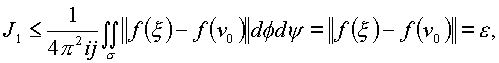
и, следовательно J₁=0, так как J₁ не зависит от R.

Окончательно можно записать, что

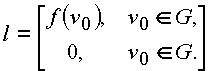
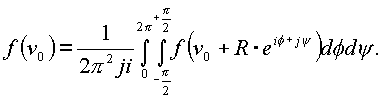
Теорема 5. (о среднем). Пусть функция дифференцируема внутри шара и непрерывна вплоть до его границы. Тогда значение этой функции в центре шара равно среднеарифметическому ее значению по поверхности, то есть

Доказательство. Положим и подставим в интеграл (1.56)

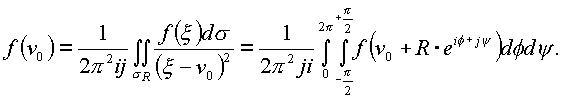
что требовалось доказать.

Формулы (1.52.), (1.56) допускают дифференцирование слева и справа (под знаком интеграла) по переменной. При этом равенство сохраняется и таким образом получается формула n -производной рассматриваемой функции как через одномерный, так и двойной интегралы. Заодно доказывается и существование производной.

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com