 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
1.3.3. Распространение интегральных теорем на многосвязные области.
Если функция
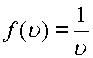 в комплексной плоскости аналитична всюду в
кольце
в комплексной плоскости аналитична всюду в
кольцеТо есть в области сферы с удаленной из нее областью изолированной оси радиуса
![]() .
.
Составим логарифмическую функцию
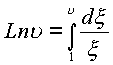 , где интеграл
будем брать по кривой
, где интеграл
будем брать по кривой Имеем
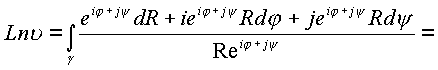
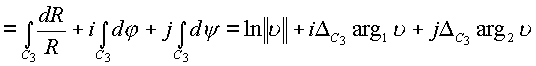 , где
, где
![]() --
приращение аргумента
--
приращение аргумента ![]() вдоль кривой
вдоль кривой![]() ,.
,.
![]() --приращение
аргумента
--приращение
аргумента ![]() вдоль кривой
вдоль кривой ![]() .
.
Многозначный характер логарифмической функции в пространстве определяется двумя аргументами. Итак
![]() . Для
замкнутой кривой
. Для
замкнутой кривой ![]()
![]() .
.
Если кривую
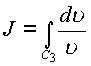 будет
равен
будет
равен
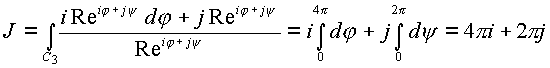
Обобщением предыдущего интеграла служит
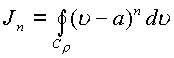 ,
где
,
где ![]() . При n=-1 интеграл равен
. При n=-1 интеграл равен
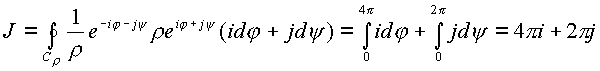
При
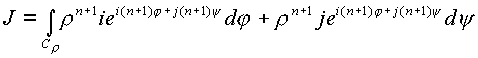 . В интеграле можно произвести
отделение комплексных частей, однако не нарушая
общего подхода в изложении, будем рассматривать
мнимые числа i, j как
обыкновенные постоянные. В этом случае к
интегралу можно применить формулу Грина.
. В интеграле можно произвести
отделение комплексных частей, однако не нарушая
общего подхода в изложении, будем рассматривать
мнимые числа i, j как
обыкновенные постоянные. В этом случае к
интегралу можно применить формулу Грина.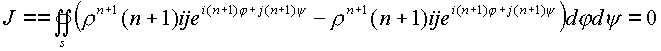
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com