 |
В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
|
10.13. Соотношение между инертной и гравитационной массой. Расчет гравитационного эффекта.
Сила, действующая на пробное тело массы
со стороны тяжелой массы (в данном случае массы земли) 
, определяется по закону Ньютона
,
где
- гравитационная постоянная, 
-расстояние пробной массы до центра Земли.
Классический закон Ньютона для тела с инертной массы
имеем соотношение
Одним из основных выводов ОТО является установления равенства инертной и гравитационной массы. В РТГ отрицается это равенство. Если в ОТО установлено равенство инертной и гравитационной массы или установлено неравенство как это происходит в РТГ, то это означает, что выявлен механизм универсального свойства материи, который связан с процессами, происходящими в пространствах псевдоримановых (в ОТО) или в пространстве Минковского (в РТГ) и как эти процессы реализуются в Евклидовом пространстве Ньютона. В силу того, что в ОТО отсутствуют законы сохранения, а гравитационное поле не является физическим Доказательство А. Эйнштейна являются необоснованными, а следовательно нет оснований считать, что в ОТО установлен механизм фундаментального свойства гравитационного поля сообщать разным массам одинаковое ускорение.
Равенство гравитационной и инертной масс установлено тщательными экспериментами с точностью не менее
их значений. 
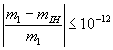
Инертная масса характеризует инертные свойства тела, а гравитационная масса - силу, с которой тела притягиваются друг к другу. Если неизвестен механизм изменения массы тел в процессе их взаимодействия, то приравнивать эти исходные формулы Ньютона нельзя, или приравняв нельзя производить сокращение
, а также приравнять ускорение
Ускорение
может скрывать изменение масс при взаимодействии.
Формулы Ньютона предполагают, что тела массами
не имеют структуры (точечные). Однако и в этом случае формула силы или потенциала описывает структуру из двух тел, так как взаимодействие осуществляется через гравитационное поле определенной энергии, сосредоточенной в пространстве между этими точками. Энергия взаимодействия –это полевая энергия с массой 
, которая движется между телами со скоростью света С по пространственной циклонной кривой типа 
(см. главу 1) и изолированному направлению, которое принадлежит пространству большего числа измерений, чем то пространство в котором находились эти тела до взаимодействия.(рис 101) За меру полевой энергии принимаем энергию обменного кванта 
. Масса обменного кванта выделяется из гравитационных масс, которые имеют свои гравитационные радиусы и изолированные направления, поэтому рассматриваем взаимодействующие структуры.
Формулы Ньютона нельзя рассматривать в Евклидовом пространстве, так как сумма
гравитационных масс до взаимодействия и при взаимодействии в этом пространстве остается без изменения. Последнее означает, что полевая энергия не имеет массы и равна нулю.
В комплексном пространстве Минковского (берем частный случай комплексного пространства) сумма гравитационных масс при взаимодействии рассчитывается по формуле
Эта масса меньше суммы исходных гравитационных масс, так как в пространстве находится полевая обменная масса
.
Эта масса перестает быть гравитационной массой, так как содержит и зависит от энергии полевого обменного кванта (вернее от гравитационного поля, созданного этими массами).
Разность в энергиях
будет характеризовать энергию инертной массы.
Поэтому потенциал Ньютона есть энергия затраченная на образование структуры при переходе масс из одного пространства измерений в другое более высокой размерности и других топологических характеристик.
Поэтому, продолжая исследования имеем формулу
(при переходе в пространстве Минковского от координат к массам)
В левой части уравнения стоит потенциал взаимодействия гравитационных масс, который является фактически дефектом этих масс, возникающим в процессе перехода в результате взаимодействия в пространство большей по величине размерности (образуется структура). В координатном исполнении это соответствует изменению модуля пространства при появлении новой временной координате.
В правой части имеем разницу в массах до взаимодействия (до образования структуры) и после взаимодействия.
В гравитационном пространстве Минковского взаимодействие осуществляется в результате появления гравитационного поля, мерой энергии которого является введенный в рассмотрение обменный квант с энергией
. Обменный квант это часть энергии масс, перешедшая в полевую энергию. За счет появления полевой энергии, которая находится в пространстве большего числа измерений, чем сумма энергий исходных масс, суммарная энергия этих масс становится меньше. Иными словами суммарная масса взаимодействующих тел в пространстве большего числа измерений становится меньше. Уменьшение фиксируется дефектом массы или потенциалом взаимодействия.
Обменный квант с физической точки зрения состоит из суммы обменного кванта
(или полевой энергии), которую выделяет пробное тело массы и обменного кванта тяжелого тела 
массы 
.
где
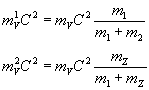
при условии
получим
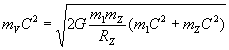
и подставив в предыдущие формулы будем иметь
,
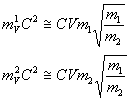где
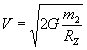
Обменный квант пробного тела составляет от общего обменного кванта при взаимодействии часть равную
. Поэтому можно считать, что гравитационная масса пробного тела равна с высокой степенью точности инерционной массе. Значение квадратного корня соответствует вышеприведенной точности экспериментальных исследований.
Однако, если пробное тело имеет скорость
относительно тяжелого тела, то его кинетическая энергия также в поле тяготения создает обменный квант 
и в этом случае также имеем
при условии
будем иметь
Обменный квант кинетической энергии вновь представляет сумму
первое слагаемое в этой сумме равно
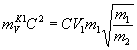
второе слагаемое равно
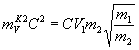
Таким образом, вид формул обменных квантов остался без изменения. Однако необходимо
иметь ввиду, что в этих формулах
.
В соответствии с моделью гравитационного взаимодействия в пространстве Минковского определим выражение для расчета инертных масс пробного и тяжелого тел.
Инертная масса тела равна гравитационной массе за вычетом массы, идущей на энергию гравитационного поля. Энергия гравитационного поля идет по изолированному направлению. Учитывая, что гравитационная масса
и его полевая масса 
находятся в комплексном пространстве, в котором 
, а модуль равен
Вводя значения обменного кванта, окончательно получим
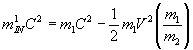
Аналогичные выкладки для тяжелого тела дают
Откуда имеем инертные массы
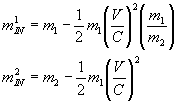
Формулы дают четкую физическую зависимость между энергией гравитационных масс и их полевыми энергиями. При взаимодействии гравитационная энергия пробного тела корректируется вычетом из нее энергии кинетической, умноженной на коэффициент отношения массы пробного тела к массе тяжелого. Гравитационная энергия тяжелого тела корректируется вычетом из нее кинетической энергии пробного тела.
Таким образом, инертная масса не равна гравитационной массе. При равенстве инертной и гравитационной массе не будет происходить образования гравитационного поля.
Теория Эйнштейна, развитая на идее искривления пространства, использовала тензорный математический аппарат, который не дает возможности адекватно реальности смоделировать и описать процесс гравитационного взаимодействия. В результате теория пришла к абсурдному выводу.
Из закона сохранения энергии имеем равенство, которое выполняется и в комплексном пространстве
В этом известном выражении сокращают массы 
как равные и получают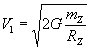 
Это первый вариант оценки равенства инертной и гравитационной массы.
Второй вариант можно провести по сравнению скорости свободного падения и скорости, входящей в выражение для кинетической энергии при не свободном движении пробного тела в поле тяжелого тела.
Подставим в исходное соотношение значение инерционной массы пробного тела
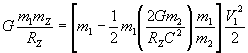
после сокращения на
получим
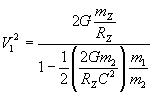в этом выражении можно воспользоваться гравитационным радиусом Шварцшильда и показать, что отрицательная величина в знаменателе второго слагаемого достаточно мала 
, поэтому
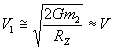
Таким образом, при соотношениях гравитационных масс
скорость пробного тела не оказывает влияния на изменение гравитационной массы.
Таким образом, процесс гравитационного взаимодействия –это процесс образования структуры более высокого порядка по пространственной размерности. Переход к новой размерности пространства происходит квантовым скачком, поэтому прав Ньютон говоря о мгновенной скорости передачи взаимодействия в этом случае. В дальнейшем идет взаимодействие внутри структуры по СТО А. Эйнштейна со скоростью света
С. Энергия гравитационного поля – эта часть энергии, которую выделяют в пространство гравитационные массы. В простейшем случае гравитационное поле является циклонным вихрем, существенным элементом которого является
-туннель, соединяющий гравитационные центры масс, через который со скоростью света проходит масса гравитационного поля (выше обозначена как обменный квант).
“Равенство инертной и гравитационной масс одного итого же тела Эйнштейн рассматривал как точный закон природы, который должен найти отражение в его теории. В настоящее время принято считать доказанным, что в общей теории относительности гравитационная масса (или, как ее иногда называют, тяжелая масса) системы, состоящей из вещества и гравитационного поля, равна его инертной массе” …”Однако этот вывод является неправильным “ А. А. Логунов
Ясно, что и гравитационная масса и инертная масса состоят и вещества и гравитационного поля. Но формулы Ньютона, (которые и ставят вопрос о равенстве гравитационной и инертных масс)
являются конкретными зависимостями межу гравитационной массой и ее инерционной массе 
, поэтому необходимо рассматривать также конкретное соотношение между ними. Понятие вещество входит как в гравитационную так и инертную массу. Вещество и является источником обменного кванта гравитационного поля. Изменяется энергия обменного кванта изменяется инерционная масса за счет изменения энергии вещества, при этом энергия вещества в процессе остается без изменения.
В соответствии с выведенными формулами зависимости инертной и гравитационной масс имеем закон сохранения масс в процессе взаимодействия
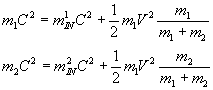
Сложим левые и правые части
Таким образом, при гравитационном взаимодействии выполняется ЗАКОН СОХРАНЕНИЯ МАСС, который выражается в виде
где 
-кинетическая энергия тела массы 
При гравитационном взаимодействии сумма гравитационных масс равна сумме инерционных масс плюс кинетическая энергия тел (в данном случае пробного тела).
Проведем дополнительные соображения, поясняющие выше приведенные выкладки.
Согласно комплексного пространства Минковского имеем
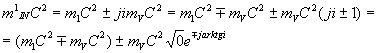
Математическая модель показывает, гравитационная масса за вычетом массы обменного кванта окружена гравитационным полем из энергии этого обменного кванта, которое принадлежит изолированному направлению (в цилиндрических координатах поле адекватно световому конусу).
Тяжелая масса
состоит из вещества 
и энергии гравитационного поля 
В комплексном представлении это выражение надо записать в виде
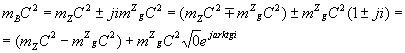
Аналогично, инертная масса
также состоит из вещества 
и энергии гравитационного поля этой массы 
. Получим выражение
В комплексной записи это будет выражение
Из этих комплексных выражений будем иметь 
Сумма второго и третьего слагаемого в правой части представляет энергию обменного кванта, которая также состоит из вещества в форме энергии поля и полевой энергии
Эти рассуждения проведены с целью продемонстрировать как один уровень пространства при взаимодействии вкладывается в другой уровень и является его комплексной составной частью. Энергия гравитационного поля, его масса порождает на новом уровне также энергию поля с массой и так до бесконечности….
Математический аппарат тензорного исчисления не обладает свойствами вложенных пространств, поэтому ОТО А. Эйнштейна привела к абсурдному выводу равенства гравитационной и инертной массы.
Таким образом, закон сохранения масс при гравитационном взаимодействии записывается в виде
Где
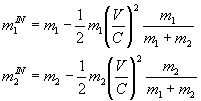
Где также
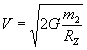
Формулы дают сохранение масс при движении пробной массы со скоростью
в поле тяготения тяжелой массы.
Формулы связи между гравитационной и инертной массами показывают, что при соотношении
массы можно приравнять даже при больших скоростях движения пробного тела 
Положение резко изменится, если взаимодействующие гравитационные массы будут примерно соизмеримы, так что положение о равенстве инертной и гравитационной массы нельзя переносить на процессы в космическом пространстве.
Гравитационное поле имеет энергетическую меру в виде обменного кванта, в состав которого входит обменный квант от кинетической энергии. В связи с этим, если произойдет резкое торможение
, так что кинетическая энергия станет равной нулю на фиксированном расстоянии
между телами, то появится избыток обменного кванта, который реализуется в изменении этого фиксированного расстояния на 
.
На расстоянии
две массы имеют гравитационный обменный квант как сумму из обменного кванта, вызванного выделением в пространство массы при мгновенном статическом положении этих масс так и массы от кинетической энергии движения пробного тела cо скоростью
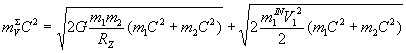
Если скорость пробного тела мгновенно погасить до нуля
, то второе слагаемое при расстоянии 
даст добавку к гравитационной массе пробного тела, так что получим
после преобразований получим
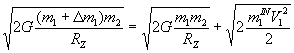
произведем сокращение
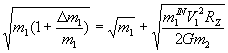
В подкоренном выражении для оценки примем
. Обменный квант от кинетической энергии перейдет при остановке в массу со скоростью света то есть будем иметь
(обменный квант реализуется через изолированное направление, так что при этом будем иметь 
).
Дальнейшие преобразования дают
Расчет проводится в два этапа. На первом этапе при мгновенной остановке пробного тела, определяем прирост величину массы пробного тела за счет реализации обменного кванта на фиксированном расстоянии между телами. Прирост массы будет величиной чисто расчетной и фиктивной, так как она вводится для определения расстояния между телами.
При этом фиктивная величина прироста гравитационной массы равна по модулю массе обменного кванта кинетической энергии. Ее реализация в изменении расстояния между телами происходит со скоростью света. Из формулы гравитационного взаимодействия Ньютона получим (при условии постоянства второй массы, изменение которой было учтено расстоянием)
при
получим 
На втором этапе учитываем как фиктивная масса реализуется в изменении расстояния между телами. Для этого составим пропорцию
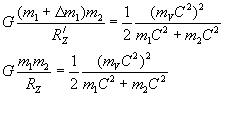
Из этой пропорции получаем
Подставляя выше вычисленное значение в изменении массы пробного тела, получим
Откуда величина сдвига (или величина гравитационного эффекта) равна
На эту величину в первом приближении должно измениться расстояние между взаимодействующими телами при мгновенной остановке тела массы
.
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: mathsru@gmail.com