1.2.2.A. Степенная функция

В. И. ЕЛИСЕЕВ

ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ ФУНКЦИЙ ПРОСТРАНСТВЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Оглавление]

Функции и где n - любое целое положительное число, определены во всем пространстве (Y).

Функция n ⁿ в пространстве (n ) за вычетом e -туннеля дискретных точек представима в следующих выражениях:

(1.31.)

откуда

где величина y и соответственно q могут быть комплексными.

Можно воспользоваться формулой (1.6), тогда

и соотношения запишутся в виде:

(1.32.)

где все параметры действительны.

Соотношения (1.31.), (1.32.) показывают, что отображение, осуществляемое функцией n ⁿ, сводится к повороту всех углов f , y , s на угол (n-1) argn и растяжению радиуса вектора в раз.

В трехмерном пространстве можно записать

Полученные соотношения не отличаются от формул (1.31.) с той лишь оговоркой, что y и q - действительные числа. В этом случае поверхность пространственного сектора на сфере r радиуса, ограниченная условиями

отображается на поверхность сферы радиуса, в раз большего, и охватывает всю поверхность сферы (рис. 14).

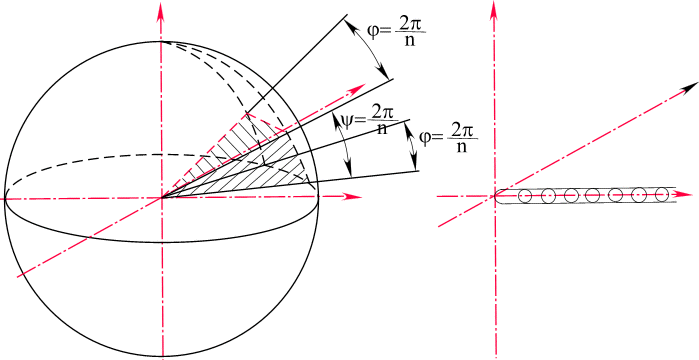
Рис. 14. Отображение пространственного сектора в полное пространство

Для однозначного отображения выкалывается ось, действительная в положительном направлении.

Докажем, что функция n ⁿ аналитична в пространстве (n ). Раскроем предел (1.21.)

Таким образом, для любого n существует предел и функция аналитична. Проверим условия дифференцирования функции на ее частном виде n ².

В цилиндрических координатах трехмерного пространства имеем

откуда

Проверяем условия дифференцирования в форме (1.26.):

Определяем производную

Таким образом, табличная производная осталась без изменения.

В цилиндрических координатах четырехмерного пространства проверяем условия дифференцируемости в формах (1.28.), (1.29.):

Отделение комплексных частей дает:

В соответствии с условиями (1.28.), (1.29.) имеем:

Определяем производную:

Таким образом, табличная производная осталась в силе.

Функция n ⁿ определена на выколотой оси, то есть в дискретных точках делителей нуля

Если

то

По-прежнему имеем

Функция является обратной функции n ⁿ.

Если

то

Соотношения, определяющие отображения, имеет вид:

Однако для этих отображений необходимо определить периодичность изменения аргументов f , y . На этом остановимся после интегральных теорем.

Для однозначных ветвей для функции существует табличная производная

(1.33.)

Функция определена и в делителях нуля. Формально можно провести операции

При операциях с такими комплексами необходимо следить за порядком нуля н коэффициентом перед изолированным аргументом.

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2.4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, "Введение в методы теории функций пространственного комплексного переменного", изданной Центром научно-технического творчества молодежи Алгоритм. - М.:, НИАТ. - 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: mathsru@gmail.com